GeometrieUndUnterrichtSS2019 04: Unterschied zwischen den Versionen
(→Nachbereitungsauftrag) |
(→Nachbereitungsauftrag) |
||
| Zeile 63: | Zeile 63: | ||
# Für die Validierung „ihres“ Approximationsverfahrens vergleicht Tai ihre Rechenergebnisse mit einem Bestimmungsverfahren für den „wahren Wert“. Diskutieren Sie die beiden Verfahren vor dem Hintergrund des ''Messen-durch-Auslegen-und-Zählen-Aspekts'', des ''Messen-als-Berechnen-Aspekts'' und des ''Vergleichsaspekt'' (vgl. Grundprinzipien des Messens in ). | # Für die Validierung „ihres“ Approximationsverfahrens vergleicht Tai ihre Rechenergebnisse mit einem Bestimmungsverfahren für den „wahren Wert“. Diskutieren Sie die beiden Verfahren vor dem Hintergrund des ''Messen-durch-Auslegen-und-Zählen-Aspekts'', des ''Messen-als-Berechnen-Aspekts'' und des ''Vergleichsaspekt'' (vgl. Grundprinzipien des Messens in ). | ||
# Analysieren Sie die Fehler/Fehlvorstellung zum ''Messen'', die in dem Artikel sichtbar werden. Skizzieren Sie Hypothesen, wie diese Fehlvorstellungen entstanden sein könnten und wie Sie Ihnen im Unterricht der Sekundarstufe II begegnen bzw. im Unterricht der Sekundarstufe I vorbeugen könnten. | # Analysieren Sie die Fehler/Fehlvorstellung zum ''Messen'', die in dem Artikel sichtbar werden. Skizzieren Sie Hypothesen, wie diese Fehlvorstellungen entstanden sein könnten und wie Sie Ihnen im Unterricht der Sekundarstufe II begegnen bzw. im Unterricht der Sekundarstufe I vorbeugen könnten. | ||
| + | |||
| + | === Ergebnisse der Nachbereitung === | ||
| + | |||
| + | Tragen Sie hier die Ergebnisse Ihrer Nachbereitung in Textform (nicht länger als 500 Wörter) ein. | ||
| + | |||
| + | === Abgabe von Max Mustermann === | ||
| + | |||
| + | Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. | ||
== Literaturhinweise == | == Literaturhinweise == | ||
Version vom 20. Mai 2019, 10:18 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Vom Volumen zum Flächeninhalt
Denken Sie sich einen mit rechtiger Innenquerschnittsfläche (Würfel, Milchkarton,…). Gesucht ist der Flächeninhalt der Innenquerschnittsfläche (Grundfläche). Zur Verfügung stehen Ihnen Wasser, eine Waage und ein Maßband.
- Wie würden Sie mit Hilfe der gegebenen Hilfsmittel den gesuchten Flächeninhalt bestimmen?
- Übertragen Sie ihr vorgehen auf Körper mit zylinder-förmiger Innenquerschnittsfläche (Tasse, Regentonne, Mülleimer,…) und auf allgemeine Zylinder.
- In dieser Aufgabe wurde das Problem der Flächenmessung auf das Problem der Volumenmessung zurückgeführt. Aus sicht der gewöhnlichen Sequenzierung der mathematischen Inhalte in der Sekundarstufe erscheint dieses Vorgehen zunächst fragwürdig. Erläutern Sie, warum das Problem der Volumenmessung im Alltag tatsächlich das einfacherere Problem ist.
Vom Flächeninhalt zum Volumen
Lesen Sie den Abschnitt „Prinzip von Cavalieri, Satz von Dehn und Pyramidenvolumen“ aus dem Skript zur „Didaktik der Mathematik in der Sek. I“, Kapitel „Didaktik der Geometrie“, von Prof. Dr. Jürgen Roth (Universität Koblenz Landau).
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit dem Satz von Cavalieri nach.
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit Stufenkörpern nach.
- Für welchen Unterrichtsgang würden Sie sich in Ihrem Unterricht entscheiden? Warum?
Vorbereitungsauftrag (Zusatz)
Der Satz von Fubini ist ein Satz über die Möglichkeit der Berechnung von Doppelintegralen durch iterative Integration:
Bearbeiten Sie die folgenden Aufträge.
- Wiederholen Sie den Satz von Fubini aus Ihrer entsprechenden Mathematik-Vorlesung (vermutlich Analysis, Maßtheorie, Wahrscheinlichkeitstheorie, Funkionalanalysis o.Ä.).
- Formulieren Sie den Satz von Fubini für folgenden Spezialfall: Es sei
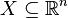 ein abgeschlossener Quader, und
ein abgeschlossener Quader, und 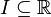 ein abgeschlossenes Intervall. Ferner sei
ein abgeschlossenes Intervall. Ferner sei 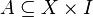 messbar. Wir betrachten für
messbar. Wir betrachten für 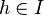 die Mengen
die Mengen 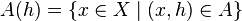 . Wie können Sie
. Wie können Sie 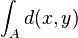 berechnen?
berechnen?
- Für das Prinzip von Cavalieri findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen.
- Welche Bestandteile der Schulbuch-üblichen Formulierung entsprechen welchen Bestandteilen der fachmathematisch präzisen Formulierung?
Das Prinzip von Cavalieri (für Körper)
Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben.
Sitzungsmaterialien
- Begleitfolien der Seminarsitzung vom 17.05.2019
- Vortragsnotizen für die Integration des Paralellograms
Dokumentation der Sitzung
Zusammenfassung
Inhaltlicher Input
Das Prinzip von Cavalieri (für Körper)
Im Raum werden zwei Körper und die Schar aller zu einer Ebene parallelen Ebenen betrachtet. Wenn für jede Ebene der Schar die beiden Schnittflächen mit den zwei Körpern gleichen Flächeninhalt haben, so sind die beiden Körper volumengleich.
Das Prinzip von Cavalieri (für Flächen)
In einer Ebene werden zwei Figuren und die Schar aller zu einer Geraden parallelen Geraden betrachtet. Wenn für jede Gerade der Schar die beiden Schnitte mit den zwei Figuren gleich lang sind, so sind die beiden Figuren flächengleich.
Arbeitsphase
Nachbereitungsauftrag
Im Jahre 1994 veröffentlichte das Journal Diabetes Care den Artikel „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“ von Mary M. Tai. In dem Artikel entwickelt und validiert Tai eine Methode zur Berechnung der Fläche unter einer Blutzuckerkurve.
- Finden Sie heraus, wann und von wem die Integrationstheorie und insbesondere die Trapezregel entwickelt wurde. Lesen Sie dann Tai (1994) „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“.
- Für die Validierung „ihres“ Approximationsverfahrens vergleicht Tai ihre Rechenergebnisse mit einem Bestimmungsverfahren für den „wahren Wert“. Diskutieren Sie die beiden Verfahren vor dem Hintergrund des Messen-durch-Auslegen-und-Zählen-Aspekts, des Messen-als-Berechnen-Aspekts und des Vergleichsaspekt (vgl. Grundprinzipien des Messens in ).
- Analysieren Sie die Fehler/Fehlvorstellung zum Messen, die in dem Artikel sichtbar werden. Skizzieren Sie Hypothesen, wie diese Fehlvorstellungen entstanden sein könnten und wie Sie Ihnen im Unterricht der Sekundarstufe II begegnen bzw. im Unterricht der Sekundarstufe I vorbeugen könnten.
Ergebnisse der Nachbereitung
Tragen Sie hier die Ergebnisse Ihrer Nachbereitung in Textform (nicht länger als 500 Wörter) ein.
Abgabe von Max Mustermann
Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet. Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua. At vero eos et accusam et justo duo dolores et ea rebum. Stet clita kasd gubergren, no sea takimata sanctus est Lorem ipsum dolor sit amet.
Literaturhinweise
- Greefrath et al. (2016) „Didaktik der Analysis“.
- Hoffmann (2018). „Konzeption von fachmathematischen Schnittstellenmodulen für Lehramtsstudierende am Beispiel ausgewählter Themen der höheren Analysis“. In khdm-Report (Masterarbeit).
- Kapitel 5 (Flächeninhalte in den Klassen 5 bis 10) in Krauter (2008). „Beiträge zur Methodik und Didaktik des Geometrieunterrichts in der Sekundarstufe 1 (Klassen 5 bis 10)“.
- siehe auch: übergreifende Literaturhinweise