GeometrieUndUnterrichtSS2019 08: Unterschied zwischen den Versionen
(→Arbeitsphase 2: verschiedene Beweise zum Satz des Pythagoras) |
(→Diskussionsphase 2) |
||
| Zeile 95: | Zeile 95: | ||
Insbesondere jedoch stellte sich am Ende der Sitzung die Frage, welches Ziel man mit dem ausgewählten Beweis verfolgt: | Insbesondere jedoch stellte sich am Ende der Sitzung die Frage, welches Ziel man mit dem ausgewählten Beweis verfolgt: | ||
| − | *'''am Zweck der Aussage orientieren''': Der Anspruch, dass im Beweis auch vorkommen sollte, was die Kernaussage des Satzes ist (z.B. Satz des Pythagoras | + | *'''am Zweck der Aussage orientieren''': Der Anspruch, dass im Beweis auch vorkommen sollte, was die Kernaussage des Satzes ist (z.B. handelt der Satz des Pythagoras von den Flächeninhalten der Quadrate über den Seiten eines rechtwinkligen Dreiecks, also wäre es sinnvoll, wenn die Flächeninhalte im Beweis aufgegriffen würden). |
| − | *'''am zukünftigen Unterricht orientieren''': Der Anspruch, dass der Beweis repräsentiert, wofür der Satz im späteren Verlauf des Unterrichts verwendet werden wird (z.B. Satz des Pythagoras i.d.R. nicht für Flächeninhaltsbestimmungen sondern Längenbestimmungen verwendet). | + | *'''am zukünftigen Unterricht orientieren''': Der Anspruch, dass der Beweis repräsentiert, wofür der Satz im späteren Verlauf des Unterrichts verwendet werden wird (z.B. wird der Satz des Pythagoras i.d.R. nicht für Flächeninhaltsbestimmungen sondern Längenbestimmungen verwendet). |
| + | |||
| + | Diese Kriterien können hilfreich sein, wenn es darum geht, den passenden Beweis eines mathematischen Satzes auszuwählen, der im Unterricht behandelt werden soll. Erst wenn das Ziel feststeht, welches mit der Unterrichtsstunde und damit insbesondere mit dem Beweis erreicht werden soll, kann die Lehrperson daran gehen, den ausgewählten Beweis für die SuS zugänglich zu machen, indem sie einzelne Schritte durch intuitive oder anschauliche Argumente ersetzt. | ||
== Nachbereitungsauftrag == | == Nachbereitungsauftrag == | ||
Aktuelle Version vom 23. Juni 2019, 14:12 Uhr
Inhaltsverzeichnis
|
Vorbereitungsauftrag
- Lesen Sie Blum & Kirsch (1991). Preformal Proving: Examples and reflections. In Educational Studies in Mathematics.
- Formulieren Sie für Sich Arbeitsdefinitionen von „Experimentellen Beweisen“, „Inhaltlich-anschaulichen Beweisen“ und „Formalen Beweisen“.
Sitzungsmaterialien
Dokumentation der Sitzung
Zusammenfassung
Die Sitzung klärt zunächst die zentrale Frage, was in der Mathematik unter einem Beweis verstanden wird und welche Funktionen dieser hat, um diese Erkenntnisse auf den Mathematikunterricht anwenden zu können. Insbesondere werden zwei Konzepte behandelt, welche helfen können, die Aspekte von mathematischen Beweisen für den Unterricht adäquat zu machen. Unter anderem spielen dabei inhaltlich-formale Beweise eine große Rolle, was sowohl im Vorbereitungsauftrag als auch in der Sitzung aufgegriffen wurde. Zwei Arbeitsphasen mit anschließender Diskussion vertiefen die Eigenschaften des inhaltlich-formalen Beweises sowie seine Realisierung im Unterricht.
Inputphase
Die zentrale Frage in der Auseinandersetzung mit dem Thema der Sitzung bildete diejenige nach der Definition eines (mathematischen) Beweises: „Unter einem mathematischen Beweis versteht man die deduktive Herleitung eines mathematischen Satzes aus Axiomen und zuvor bereits bewiesenen Sätzen nach spezifizierten Schlussregeln. Axiome sind unbewiesene Aussagen, die man an den Anfang einer Theorie stellt.“
Was ist ein Beweis?
Ein mathematischer Beweis leitet also die Aussage eines Satzes aus bereits bewiesenen Erkenntnissen her und verwendet dabei Prinzipien und Regeln, welche von der „Scientific Community“ festgelegt beziehungsweise vereinbart wurden. Dazu gehören unter anderem die folgenden drei Prinzipien:
- Lückenlosigkeit und Vollständigkeit: Mathematische Beweise basieren auf Voraussetzungen, Axiomen und bereits bewiesenen Sätzen, sind nachvollziehbar, vollständig (lassen keinen Schritt aus) und korrekt.
- Minimalität: Mathematische Beweise sind ästhetisch und so kurz wie möglich, d.h. sie verwenden so wenig Argumente wie nötig und doppeln sich nicht in ihrer Formulierung.
- Formalisierung von Struktur, Sprache und Symbolik: Mathematische Beweise folgen einer formalisierten, also größtenteils vereinheitlichten Struktur und verwenden vereinheitlichte Sprache (z.B. Formulierungen) und Symbolik. Dadurch ist ein mathematischer Beweis unabhängig von der Sprache, in der er verfasst wurde, für den Mathematiker leichter zugänglich und nachvollziehbar.
Es muss jedoch berücksichtigt werden, dass die Einhaltung dieser Prinzipien nicht immer vollständig erfolgt. Im Kontext von Schule ist es offensichtlich nicht dienlich, ausschließlich mit mathematischen, also formalen Beweisen, zu arbeiten. Aber auch in der mathematischen Praxis wird längst nicht jeder Beweis vollständig und lückenlos geführt.
Funktionen des Beweisens
- Verifikation: Beweise dienen dazu, zu verifizieren, dass eine bestimmte Behauptung gültig ist. Dieser Punkt lässt gewisse Fragen zu. Insbesondere muss das Argument berücksichtigt werden, dass der Mathematiker in der Regel bereits überzeugt ist, dass die Aussage gilt, die er beweisen möchte. Im Seminar wurde die Frage gestellt, ab wann der Mathematiker mit einem Beweis anfängt – wenn er sich zu 99% sicher ist, dass er stimmt oder wenn er dahingehend erst eine grobere Vermutung hat. Die Antwort verwies auf bestimmte mathematische Sätze (z.B. großer Satz von Fermat), deren Richtigkeit lange Zeit grundsätzlich angenommen wurde, auch wenn der Beweis zu diesem Zeitpunkt noch nicht geliefert war. Zudem wurde argumentiert, dass man sich selten unsicher ist, ob eine Aussage tatsächlich gilt, wenn man versucht, sie zu beweisen.
- Erklärung: Beweise sollen erklären, warum eine Behauptung gilt, also den Kern der mathematischen Aussage festhalten.
- Einordnung und Systematisierung: Was kann aus dem Beweis bzw. der bewiesenen Aussage gefolgert werden? Welche Voraussetzungen brauchen wir, welche Sätze und Axiome können / wollen wir verwenden?
- Kommunikation und Verbreitung mathematischen Wissens: Beweise ermöglichen das sprachenübergreifende Notieren mathematischer Argumente, die Kommunikation zwischen Mathematikern und das Aufbauen eines Formalisierungssystems.
Im Kontext des Schulunterrichts kommen außerdem folgende Aspekte hinzu:
- Rationales Argumentieren und Überzeugen: Beweise haben einen Adressaten, der von der Richtigkeit der Aussage überzeugt werden soll.
- Erkennen und Erkunden von Zusammenhängen, Konsequenzen von Definitionen und Annahmen: Was geschieht, wenn wir eine bestimmte Annahme weglassen oder den Beweis modifizieren? Mit welchen Definitionen arbeiten wir und welche Konsequenzen hat das für den Beweis?
- Aufstellen neuer Vermutungen: Welche neuen Fragestellungen, Folgerungen, Probleme ergeben sich?
Argumentieren und Beweisen in der Schule
Wie können die drei Prinzipien des mathematischen Beweises auf die Schule angewandt werden? An dieser Stelle helfen die folgenden Konzepte:
| Prinzip des mathematischen Beweises | Konzept zur Umsetzung im Unterricht | Erklärung |
|---|---|---|
| Lückenlosigkeit und Vollständigkeit | Lokales Ordnen statt globalem Ordnen | Aus verschiedenen Gründen (u.a. verfügbare Zeit und Wissensstand der SuS) kann in der Schule nicht jede Erkenntnis auf Axiome zurückgeführt werden. Stattdessen kann das lokale Beweisen eine gute Möglichkeit für den Unterricht sein. Beispielsweise wird hierbei gefragt, in welcher Beziehung verschiedene Sätze zueinander stehen, ohne sie selbst auf Axiome zurückzuführen. |
| Minimalität | Redundanzen und vielfältige Zugänge, individuell sinnstiftende Darstellungen | Der Schulunterricht verlangt nach Anschauungen und ggf. unterschiedlichen Erklärungen oder Zugängen bei Verständnisproblemen. Auch das individuelle Lernen und und Arbeiten (z.B. Kostruieren) sollte hier eine wichtige Rolle spielen. |
| Formalisierung von Struktur, Sprache und Symbolik | Inhaltlich-anschauliche Beweise statt rigorosem Formalismus | siehe nächster Abschnitt |
Diskussionsphase 1: Inhaltlich-anschauliche Beweise
Erbegnisse des Vorbereitungsauftrags
Einige Beispiele von Arbeitsdefinitionen experimenteller, inhaltlich-anschaulicher und formaler Beweise:
- experimenteller Beweis: "Ein experimenteller Beweis findet nicht in der (mathematisch-formal) korrekten Reihenfolge statt."; "Ein experimenteller Beweis überprüft die Gültigkeit einer Aussage an einem konkreten Beispiel, ohne dabei verallgemeinerbare Aussagen über die Gültigkeit treffen zu können."
- inhaltlich-anschaulicher Beweis: "Ein inhaltlich-anschaulicher Beweis besteht aus einer Kette korrekter, aber nicht formell repräsentierter Lösungen und basiert dabei auf den Erfahrungen der SuS."; "Der inhaltlich-anschauliche Beweis folgt in seiner Struktur den nötigen Schritten eines formalen Beweises, schafft es jedoch nicht, sie alle formal zu beweisen, sondern ersetzt sie gegebenenfalls durch intuitive oder anschauliche Realisierungen."
- formaler Beweis: "Ein formaler Beweis verwendet formelle Schreibweise und ist dadurch besonders kurz und prägnant."; "Ein formaler Beweis folgt den mathematisch korrekten und nötigen Schritten, um die Aussage zu zeigen."
Die Diskussion bezog sich auf die Definition inhaltlich-anschaulicher Beweise und ihre Beziehung zu experimentellen und formalen Beweisen (siehe Definition oben). Man war sich darüber einig, dass der inhaltlich-anschauliche Beweis zwischen den beiden anderen Beweistypen zu verorten ist, jedoch entstand Uneinigkeit darüber, an welchem der beiden anderen Typen er näher dran ist. Insbesondere kam der Begriff „richtiger Beweis“ auf, welcher ausführlich diskutiert wurde. Aspekte wie Gültigkeit, Formalität, Vollständigkeit und intuitive Richtigkeit wurden als mögliche Merkmale eines „richtigen Beweises“ genannt.
Die folgende Arbeitsphase diente dem Zweck, das Konzept des inhaltlich-anschaulichen Beweises zu verdeutlichen:
Arbeits- und Diskussionsphase 2
Arbeitsauftrag: Beweisen Sie den Satz (siehe Bild "Aufgabenstellung") formal und diskutieren Sie die Art des Beweises sowie mögliche inhaltlich-anschauliche Beweise.
Zunächst wurde der formale Beweis des Satzes besprochen (siehe Bild "formaler Beweis")
Die Diskussion drehte sich im Kern um die Frage, ob der Schritt der Dreiecksungleichung oder das Addieren der unterschiedlichen Längen für die SuS größere Verständnisprobleme verursachen könnten und daher durch einen inhaltlich-anschaulichen Beweis ersetzt werden sollten. Zu diesem Punkt existierten unterschiedliche Ansichten.
Eine mögliche Realisierung wurde vom Dozenten vorgeschlagen: Spannt man ein Gummiband auf einem Nagelbrett zwischen zwei Nägel, sodass es eine Strecke symbolisiert, und zieht diese dann zu einem Dreieck auf, so wird dem Betrachter intuitiv klar, dass sich die Gesamtlänge der so entstandenen Katheten des Dreiecks vergrößert hat. Führt man dieses Vorgehen bei zwei sich überschneidenden Strecken (gebildet durch Gummibänder) durch, so ergibt sich die Aussage intuitiv für das konvexe Viereck.
Zwischenfazit
Teile des mathematischen, also formalen Beweises dürfen durch ikonische oder anschauliche Argumente (z.B. eine Zeichnung, eine Simulation oder eine Handlung) ersetzt werden. Dadurch bleibt er allgemein gültig, erfüllt jedoch nicht mehr die formalen Anforderungen an einen mathematischen Beweis. Einen solchen Beweis nennt man inhaltlich-anschaulichen Beweis. Die Lehrkraft sollte also ausgehend vom mathematischen Beweis überlegen, welche Schritte anschaulich darstellbar sind, um den Beweis für die SuS zugänglich zu machen.
Arbeitsphase 2: verschiedene Beweise zum Satz des Pythagoras
Grundlage dieser Arbeitsphase war die Erkenntnis, dass für viele Sätze der Mathematik mehrere formale Beweise existieren, aus denen die Lehrperson den geeigneten auswählen muss.
Arbeitsauftrag: Sichten Sie die verschiedenen Beweise zum Satz des Pythagoras. Ist eine Formalisierung der Argumente in der Schulgeometrie möglich bzw. sinnvoll? Für welchen Beweis würden Sie sich in Ihrem Unterricht entscheiden?
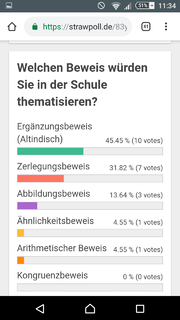
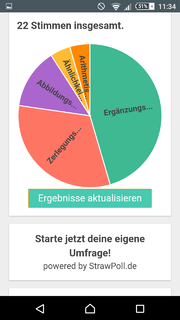
Ergebnisse der Umfrage: siehe Bilder
Diskussionsphase 2
Zu Beginn der Diskussionsphase drehten sich die Beiträge um die Frage, ob das Prinzip des Zerlegens und Ergänzens als exemplarischer oder inhaltlich-anschaulicher Beweis eingeordnet werden soll. Hintergrund waren insbesondere die Beweise 3 und 4, welche das Zerlegungsprinzip bemühen. Diese Frage wurde durch einen Beitrag des Dozenten gelöst, welcher darauf hinwies, dass auch bei der Verwendung von „Zerlegen und Ergänzen“ (beispielsweise mithilfe von Schere und Papier) dokumentiert werden muss, wie der Beweis vorgeht und welche Argumente verwendet werden. Auch das Ausschneiden kann also ein inhaltlich-anschaulicher Beweis sein, wenn dieser gut dokumentiert wird. Im weiteren Verlauf verlagerte sich die Diskussion auf die Frage, warum die Mehrheit der Seminarteilnehmer die Beweise 4, 3 und 2 für den Unterricht verwenden würde. Angeführt wurde insbesondere das Argument der Anschaulichkeit. Auch die Bevorzugung regelmäßiger geometrischer Objekte gegenüber unregelmäßiger Objekte (z.B. Trapeze) wurde genannt. Insbesondere jedoch stellte sich am Ende der Sitzung die Frage, welches Ziel man mit dem ausgewählten Beweis verfolgt:
- am Zweck der Aussage orientieren: Der Anspruch, dass im Beweis auch vorkommen sollte, was die Kernaussage des Satzes ist (z.B. handelt der Satz des Pythagoras von den Flächeninhalten der Quadrate über den Seiten eines rechtwinkligen Dreiecks, also wäre es sinnvoll, wenn die Flächeninhalte im Beweis aufgegriffen würden).
- am zukünftigen Unterricht orientieren: Der Anspruch, dass der Beweis repräsentiert, wofür der Satz im späteren Verlauf des Unterrichts verwendet werden wird (z.B. wird der Satz des Pythagoras i.d.R. nicht für Flächeninhaltsbestimmungen sondern Längenbestimmungen verwendet).
Diese Kriterien können hilfreich sein, wenn es darum geht, den passenden Beweis eines mathematischen Satzes auszuwählen, der im Unterricht behandelt werden soll. Erst wenn das Ziel feststeht, welches mit der Unterrichtsstunde und damit insbesondere mit dem Beweis erreicht werden soll, kann die Lehrperson daran gehen, den ausgewählten Beweis für die SuS zugänglich zu machen, indem sie einzelne Schritte durch intuitive oder anschauliche Argumente ersetzt.
Nachbereitungsauftrag
Literaturhinweise
- Blum & Kirsch (1991). Preformal Proving: Examples and reflections. In Educational Studies in Mathematics.
- Meyer & Prediger (2009). Warum? Argumentieren, Begründen, Beweisen (Preprint). In Praxis der Mathematik in der Schule 51(30).