GeometrieUndUnterrichtSS2019 12: Unterschied zwischen den Versionen
(→Beweisfindung und inhaltlich-anschauliche Argumente) |
(→Entdecken und Formulieren vom Satz des Thales) |
||
| Zeile 57: | Zeile 57: | ||
== Entdecken und Formulieren vom Satz des Thales == | == Entdecken und Formulieren vom Satz des Thales == | ||
| − | + | Die Klasse wird in drei Gruppen geteilt. Gruppe 2 beschäftigt sich mit der Aussage vom Satz des Thales, wohingegen Gruppe 1 und 3 die Umkehrung erforschen. <br /> | |
| + | SchülerInnen der ersten Gruppe erhalten neben dem Aufgabenblatt Overheadprojektor-Folien mit der schon vorgezeichneten Seite c des Dreiecks ABC, s.d. möglichst zügig gearbeitet werden kann. Die SuS sollen sich in der Gruppe austauschen und organisieren, wer welche Winkelgröße \beta in seinem/ihren Dreieck realisiert. Damit es nicht zu viel Folien sind, soll jeder Schüler/ jede Schülern der Gruppe mindestens zwei rechtwinklige Dreiecke mit unterschiedlichen Winkelgrößen für \beta mit Hilfe des Geodreiecks konstruieren. Danach sollen die Folien aufeinander gelegt werden, d.h. die SuS müssen zusammenarbeiten und überlegen, welche Bedingung (Seite c auf Seite c oder Rechte Winkel auf rechte Winkel) sie invariant halten möchten. Durch das Sammeln mehrerer unterschiedlicher, rechtwinkliger Dreieck mit gleicher Hypotenuse sollte die Vermutung der Umkehrung des Satz des Thales wecken, nämlich das der Eckpunkt C auf einer Kreislinie liegen muss (Seite c wird auf Seite c gelegt) oder das die Seiten c Durchmesser eines Kreises sind (Rechte Winkel werden aufeinander gelegt). Am Schluss soll ihre Vermutung auch kurz schriftlich festgehalten werden, damit im weiteren Verlauf der Unterrichtssequenz bei Behandlung der Umkehrung darauf verwiesen und die Vermutung mit dem Umkehrung des Satz des Thales verglichen werden kann. | ||
[[Datei:Arbeitsergebnis SatzEntdecken.pdf|thumb|Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Entdecken und Erarbeiten der Aussage vom Satz des Thales“]] | [[Datei:Arbeitsergebnis SatzEntdecken.pdf|thumb|Ergebnis (Arbeitsblatt) zum Arbeitsauftrag: „Entdecken und Erarbeiten der Aussage vom Satz des Thales“]] | ||
Version vom 5. Juli 2019, 14:53 Uhr
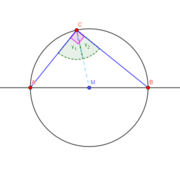
Der Satz des Thales und formaler Beweis
Mögliche Formulierung: „Alle Winkel an einem Halbkreis sind rechte Winkel“.
Formaler Beweis
Es ist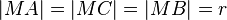 
,
wobei r den Radius des Kreises bezeichnet. Demnach sind ΔAMC und ΔMBC gleichschenklig.
Insbesonders gilt aufgrund des Basiswinkelsatzes für gleichschenklige Dreiecke: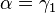 
und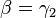 
.
Wegen des Satzes der Winkelsumme im Dreieck ΔABC gilt:
,
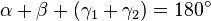und mit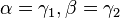 
ergibt sich
.
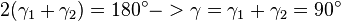Vorüberlegungen
Bereitstellung und/oder Aktivierung von Vorwissen der Schülerinnen und Schüler
Zunächst stellte sich die Frage, welches Vorwissen bei den SuS vorhanden sein und aktiviert werden muss. Dies wurde an der Tafel zusammengetragen:
- Alle Punkte auf einer Kreislinie haben den gleichen Abstand zum Kreismittelpunkt
- Basiswinkelsatz für gleichschenklige Dreiecke
- Satz über Winkelsumme im Dreieck, Rechnen mit Winkeln (Addierbarkeit, Ergänzung von Winkeln)
- Lösungsverfahren von Gleichungen, speziell Einsetzungsverfahren
- Definition & Eigenschaften von gleichschenkligen Dreiecken
Anschließend wurde diskutiert, wie man dieses Vorwissen aktivieren könne, im Hinblick auf den möglichen Zeitaufwand zu Beginn einer Unterrichtsstunde. Genannt wurden Besprechung von Hausaufgaben, Kurzteste oder -abfragen sowie ein Quizz zu beginn. Für letzteres sollten Fragen entworfen werden, die im Idealfall aus Zeitgründen kompakt, aber dennoch alles abdecken sollten. Beispiele waren:
- Was ist ein Kreis?
- Was ist ein (gleichschenkliges) Dreieck?
- Wieviele rechte Winkel kann ein Dreieck haben?
Allerdings wurden auf den Einwand hin, dass eventuell Schwierigkeiten dabei auftreten könnten, den Bezug dieses Wissen zum Beweis zu sehen, noch bildliche Beispiele genannt, die in Richtung der obigen Skizze des Beweises gingen. Hierbei könnte man fragen: "Wie lang ist |AB|?" usw.
Finden und Formulieren der Vermutung (zum Satz des Thales)
Explorieren oder Operatives Durcharbeiten der Problemsituation
Beweisfindung und inhaltlich-anschauliche Argumente
Formalisierung der Beweisargumentation
Rückschau, operatives Durcharbeiten des Beweises
Kollaborative Unterrichtsskizze zur Beweisaufgabe: „Satz des Thales“
Aktivierung von Vorwissen
Entdecken und Formulieren vom Satz des Thales
Die Klasse wird in drei Gruppen geteilt. Gruppe 2 beschäftigt sich mit der Aussage vom Satz des Thales, wohingegen Gruppe 1 und 3 die Umkehrung erforschen.
SchülerInnen der ersten Gruppe erhalten neben dem Aufgabenblatt Overheadprojektor-Folien mit der schon vorgezeichneten Seite c des Dreiecks ABC, s.d. möglichst zügig gearbeitet werden kann. Die SuS sollen sich in der Gruppe austauschen und organisieren, wer welche Winkelgröße \beta in seinem/ihren Dreieck realisiert. Damit es nicht zu viel Folien sind, soll jeder Schüler/ jede Schülern der Gruppe mindestens zwei rechtwinklige Dreiecke mit unterschiedlichen Winkelgrößen für \beta mit Hilfe des Geodreiecks konstruieren. Danach sollen die Folien aufeinander gelegt werden, d.h. die SuS müssen zusammenarbeiten und überlegen, welche Bedingung (Seite c auf Seite c oder Rechte Winkel auf rechte Winkel) sie invariant halten möchten. Durch das Sammeln mehrerer unterschiedlicher, rechtwinkliger Dreieck mit gleicher Hypotenuse sollte die Vermutung der Umkehrung des Satz des Thales wecken, nämlich das der Eckpunkt C auf einer Kreislinie liegen muss (Seite c wird auf Seite c gelegt) oder das die Seiten c Durchmesser eines Kreises sind (Rechte Winkel werden aufeinander gelegt). Am Schluss soll ihre Vermutung auch kurz schriftlich festgehalten werden, damit im weiteren Verlauf der Unterrichtssequenz bei Behandlung der Umkehrung darauf verwiesen und die Vermutung mit dem Umkehrung des Satz des Thales verglichen werden kann.
Exploration der Phänomensituation (Thalesfiguren)
Beweisfindung und Argumentation
