GeometrieUndUnterrichtSS2019 10: Unterschied zwischen den Versionen
(→Beispiel) |
(→Ergebnisse des Nachbereitungsauftrags) |
||
| Zeile 155: | Zeile 155: | ||
Zur Vertiefung des Themas „Achsenspiegelung“ fertigen SuS Scherenschnitte an und konstruieren somit selbst achsensymmetrische Figuren. In den Scherenschnitten können Winkel- und Längeneigenschaften sowie die Lagebeziehung von Punkten genauer untersucht werden. Anschließend könnte die Lehrperson nur einen Ausschnitt eines Scherenschnittes austeilen, den die SuS in ihr Heft einkleben sollen. Aufgabe soll sein, den Rest der achsensymmetrischen Figur einzuzeichnen. | Zur Vertiefung des Themas „Achsenspiegelung“ fertigen SuS Scherenschnitte an und konstruieren somit selbst achsensymmetrische Figuren. In den Scherenschnitten können Winkel- und Längeneigenschaften sowie die Lagebeziehung von Punkten genauer untersucht werden. Anschließend könnte die Lehrperson nur einen Ausschnitt eines Scherenschnittes austeilen, den die SuS in ihr Heft einkleben sollen. Aufgabe soll sein, den Rest der achsensymmetrischen Figur einzuzeichnen. | ||
| + | |||
| + | ==== Nachbereitungsauftrag Anna-Lena ==== | ||
| + | ===== Vorteile des abbildungsgeometrischen Ansatzes ===== | ||
| + | * Verknüpfung des Abbildungsbegriffs mit dem Gruppenbegriff | ||
| + | * Darbietung von handlungsbezogenen Zugängen aufgrund dynamischer Eigenschaft des abbildungsgeometrischen Ansatzes (-> Bewegungsgeometrie + freie Beweglichkeit des starren Körpers) | ||
| + | * Möglichkeit von globalen und lokalen Ordnungsstrukturen (Projektive Geometrie -> Euklidische Geometrie -> Darstellende Geometrie; Invarianzbetrachtungen; beliebige Elementarisierung in Beweisen möglich) | ||
| + | |||
| + | ===== Beispiel ===== | ||
| + | Die SuS sollen regelmäßige geometrische Objekte (gleichseitiges Dreieck, Quadrat, Pentagon, Hexagon, Tetraeder, evtl. Oktaeder, Kegel, Zylinder) auf Spiegelebenen, Dreh- und Drehspiegelachsen enaktiv mit Modellen untersuchen. Durch begleitende Fragestellungen wie | ||
| + | * Welche Operationen/Handlungen können die Figur in eine nicht unterscheidbare Figur überführen, d.h. Eckpunkte auf andere Exkpunkte und Kanten auf Kanten? | ||
| + | * Wie oft muss ich die Operation durchführen, um bei der Usprungsfigur zu landen? | ||
| + | * Ist es möglich Operationen zu einer Operation zusammenzufassen? Wenn ja, welche? | ||
| + | * Was passiert mit den Punkten der einer verkleinerten oder vergrößerten Figur unter der Operation? | ||
| + | * Was passiert mit einem Punkt im Raum der nicht auf der Figur liegt? | ||
| + | * Welche Punkte im Raum/Ebene werden durch die ausgeführte Operation/Handlungen festgehalten? | ||
| + | sollen die SuS enaktiv | ||
| + | * Gruppeneigenschaften von einfachen, meist endlichen Symmetriegruppen erfahren | ||
| + | * den linearen, funktionalen Charakter von geometrischen Abbildungen erfahren | ||
| + | * Invarianten von Drehungen, Spiegelungen und Drehspiegelungen kennenlernen | ||
| + | |||
| + | Es wäre sinnvoll, dass der Lehrer ein Beispiel im Plenum vorführt und die Sus in Gruppen je eine Figur bzw. Körper untersuchen. | ||
== Literaturhinweise == | == Literaturhinweise == | ||
Version vom 19. Juli 2019, 07:21 Uhr
Sitzungsmaterialien
Dokumentation der Sitzung
Aufwärmübung
Als Aufwärmübung hatten wir eine Gerade mit 3 Punkten, von denen zwei nicht auf der Gerade lagen und sich auf der gleichen Seite der Gerade befanden. Der dritte Punkt war ein beliebiger Punkt auf der Gerade. Die Gerade war ein Fluss und die anderen beiden Punkte waren Bob und Alice. Die Frage war nun, welches die kürzeste Strecke von Alice zu Bob ist.
Die ersten Vorschläge waren:
- Der kürzeste Weg ist der, bei dem die Strecke Alice - Fluss und Fluss - Bob den gleichen Abstand haben.
Daraufhin gab es einen Hinweis: Angenommen wir wollen von Alice zu Bob. Was wäre dort die kürzeste Strecke? - Die direkte Verbindung
- Alice soll den Mittelpunkt eines Kreises darstellen. Die Strecke Alice - Bob bildet den Radius. Der Punkt, an dem sich der Kreis und die Gerade Fluss schneiden, soll den Punkt auf der Gerade darstellen - Frage: Wenn es zwei Schnittpunkte gibt, welches ist der richtige Punkt? Gibt es eine kürzere Verbindung?
- Man zieht eine Senkrechte von Bob zum Fluss. Der Schnittpunkt mit der Geraden stellt den Punkt dar, wo man den Fluss überqueren soll. Auch hier: Gibt es eine kürzere Verbindung?
Lösung:
Man spiegelt den Punkt Bob an der Gerade Fluss (Fluss = Spiegelgerade). Anschließend zieht man eine direkte Verbindung von Alice zum Spiegelpunkt Bob'. Der Schnittpunkt der Strecke Alice - Bob' mit der Geraden Fluss ist der dritte Punkt. Anschließend wird zurückgespiegelt. Der kürzeste Weg ist dann von Alice zum Schnittpunkt der Strecke Alice-Bob' zu Bob.
Abbildungsgeometrischer Zugang
Die Geometrischen Abbildungen in der Euklidischen Anschauungsebene sind Längentreue Abbildungen, aus denen Winkeltreue Abbildungen und Geradentreue Abbildungen folgen. Aus den Winkeltreuen Abbildungen lassen sich die Streckenverhältnistreuen Abbildungen ableiten und aus den Geradentreuen Abbildungen, die Parallelentreue und die Teilverhältnistreuen Abbildungen.
Bei den Winkeltreuen und Streckenverhältnistreuen Abbildungen geht es insbesondere um:
- zentrische Streckungen
- Strahlensätze
- Teilung/Vervielfältigung von Strecken
Bei den Längentreuen Abbildungenn unterscheidet man zwischen ,,eigentlichen Bewegungen, wie die Verschiebung und die Drehung und den ,,uneigentlichen Bewegungen, wie den Spiegelungen und den Schubspiegelungen. Dabei spielen die umeigentlichen Bewegungen wie Spiegelung und Schubspiegelung schon in der Grundschule eine Rolle. Die Klassifikation von geometrischen Figuren durch Deckabbildungen ist zur heutigen Zeit verschwunden in den Schulen.
Begriffe der Abbildungsgeometrie in der Schule
In der Schule unterscheidet man zwischen Kongruenzabbildungen, Ähnlichkeitsabbildungen und Affinen Abbildungen.
Zu den Kongruenzabbildungen gehören:
- Verschiebungen (z.B. Vektoren)
- Drehungen (z.B. Winkel)
- Spiegelungen
- Symmetrie (z.B. Achsen- und Punktsymmetrie)
- Haus der Vierecke (Deckabbildungen)
Zu den Ähnlichkeitsabbildungen gehören:
- zentrische Streckung (Jede Ähnlichkeitsabbildung lässt sich durch eine zentrische Streckung verändern)
- erster und zweiter Strahlensatz (Der erste und zweite Strahlensatz kann in der Schule nicht gut bewiesen werden, da man intuitiv die Strahlensätze beispielsweise beim Beweis der zentrischen Streckung schon benutzt, ohne sie zuvor zu beweisen)
- Strecken teilen und vervielfältigen
Die Affinen Abbildungen sind kein Thema mehr in der Schule. Es werden nur noch teilweise Teilverhältnisse thematisiert.
Beispiel: Sätze über Teilverhältnisse.
Man kann die Seitenhalbierenden eines Dreiecks bilden und sieht, dass sich die Seitenhalbierenden im Verhältnis 2:1 schneiden. Diese Ähnlichkeit der beiden Dreiecke kann man nutzen, um das Verhältnis 2:1 zu zeigen. Dreieck ABD ist ähnlich zu Dreieck AFE, weil sie im rechten Winkel und einem zweiten Winkel übereinstimmen (Winkelsummensatz: Wenn zwei Winkel gleich sein, ist der dritte ebenso identisch). Die Ähnlichkeit ist definiert über zwei, bzw. drei gleiche Winkel. Durch die Affinität der Seitenhalbierenden, kann man dies in jedem Dreieck erzeugen.
Zusammenfassung: Gründe für die Abbildungsgeometrie
- Universelle mathematische Idee: Abbildung und Gruppen
- Funktionales Denken: Dynamische und elementarkinematische Denkweise
- Anschaulichkeit und Handlungsbezogenheit: SuS-Aktivitäten möglich(er)
- Strukturverwandschaft mit allgemeinen Denkhandlungen
- Globale Ordnung: durchgängiges Prinzip beim Geometrietreiben
- Lokale Ordnung: Abbildungsbeweise auf verschiedenen Stufen der Strenge möglich
Arbeitsphase
Bearbeitungsauftrag (Zentrische Streckungen)
- Beschreiben Sie die Konstruktion einer zentrischen Streckung angewendet auf den Punkt P für den Fall, dass Abbildungsverhalten durch einen Punkt und seinen Bildpunkt vorgegeben ist.
- Beschreiben sie die Konstruktion einer zentrischen Streckung angewendet auf den Punkt P mit rationalem Streckfaktor k =n/m
Konstruktionsbeschreibung:
- Hilfsgerade g durch Z zeichnen
- beliebiges r auf g m-mal abtragen
- m-ten Schnittpunkt Q mit P verbinden
- Parallele durch n-ten Schnittpunkt (R) zu PQ zeichnen
- Schnittpunkt von ZP und Parallele n ist Bildpunkt P'
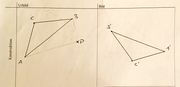
Bearbeitungsauftrag (Kongruenzabbildungen)
- Zeigen Sie, dass eine Kongruenzabbildung bereits durch ihr Verhalten auf einem Dreieck eindeutig bestimmt ist. Konstruieren Sie dazu den Bildpunkt P.
- Funktioniert Ihre Konstruktionsbeschreibung auch, wenn P an einem anderen Ort liegt? (Innerhalb des Dreiecks, auf dem Dreieck)
Konstruktionsbeschreibung:
- Kreis1 um B mit Radius BP
- Kreis2 um A mit Radius AP
- Schnittpunkt von K1 und K2{P1, P2}
- Wähle P nun so, wie das Verhalten von C zur Strecke AB ist.
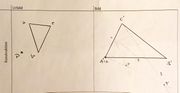
Bearbeitungsauftrag (Ähnlichkeitsabbildung)
- Zeigen Sie, dass eine Ähnlichkeitsabbildung bereits durch ihr Verhalten auf einem Dreieck eindeutig bestimmt ist. Konstruieren Sie dazu den Bildpunkt von P.
- Funktioniert Ihre Konstruktionsbeschreibung auch, wenn P an einem anderen Ort liegt? (Innerhalb des Dreiecks, auf dem Dreieck)
Konstruktionsbeschreibung:
- Dreieck ABC in Dreieck A'B'C' abtragen -> B ist Element der Strecke A'B', C ist Element der Strecke A'C' und A = A'
- Gerade durch A' und P und Gerade durch C und P
- Parallele zur Strecke CP durch C' ist g
- Schnittpunkt von g und der Strecke A'P ist P'
Alternativ kann man auch den Winkeln PAB und PBA in das Dreieck A'B'C' abtragen. Der Schnittpunkt ist dann P'
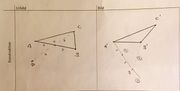
Bearbeitungsauftrag (Affinitätsabbildung)
- Zeigen Sie, dass eine Affinitätsabbildung bereits durch ihr Verhalten auf einem Dreieck eindeutig bestimmt ist. Konstruieren Sie dazu den Bildpunkt P.
- Funktioniert Ihre Konstruktionsbeschreibung auch, wenn P an einem anderen Ort liegt? (Innerhalb des Dreiecks, auf dem Dreieck)
Nachbereitungsauftrag
Lesen Sie in Bender (1982) Abbildungsgeometrie in der didaktischen Diskussion die Seiten 17 bis 18 (Abschnitt 2.6 Zusammenfassung der Begründung und Abschnitt 3 Ist Abbildungsgeometrie in der Sekundarstufe I didaktisch sinnvoll? bis Argument A).
- Formulieren Sie in eigenen Worten, welche Vorteile Sie in dem abbildungsgeometrischen Zugangs zur Geometrie sehen.
- Skizzieren Sie einen möglichen Themenausschnitt/SuS-Aktivität/…, von der Sie sich gut vorstellen könnten, diese mit einem abbildungsgeometrischen Zugang später selber zu unterrichten.
Ergebnisse des Nachbereitungsauftrags
Nachbereitungsauftrag Ilona Rein
Vorteile des abbildungsgeometrischen Ansatzes
- Einführung von Begriffen wie Abbildung und Gruppe (maßgebliche Begriffe - zumindest in der Universitätsmathematik)
- globale Ordnung: Abbildungen als Prinzip, das im Mathematikunterricht immer wieder vorkommt / vorkommen kann ("durchgängiges Prinzip der Geometrie")
- Erarbeitung von Axiomensysstemen
- ggf. erscheinen abbildungsgeometrische Beweise den SuS mächtiger / sind ihnen einsichtiger als andere Arten des Beweises eines bestimmten Resultats (Anschaulichkeit / Nachvollziehbarkeit)
Beispiel
Eine Möglichkeit wäre es, die Gleichseitigkeit eines Dreiecks mit der Achsensymmetrie an den Mittelsenkrechten in Verbindung zu bringen. Hierbei könnte auf bereits existierendes Vorwissen zur Eigenschaft gleichseitiger Dreiecke aufgebaut werden, um den Begriff der Achsensymmetrie als Abbildung einzuführen, bei der jedem Punkt des Dreiecks der Spiegelpunkt bezüglich einer Mittelsenkrechten zugewiesen wird. Die SuS müssten sich über die "Abbildungsvorschrift" Gedanken machen und könnten diese ggf. formulieren anhand ihres (hoffentlich vorhandenen) Wissens über Achsensymmetrie. Zugleich wäre mit dieser Herangehensweise die Erkenntnis verbunden, dass die Achsensymmetrie bezüglich aller drei Mittelsenkrechten gilt. Interessant wäre ausgehend von dieser Erkenntnis auch die Möglichkeit, nach den Symmetrien in gleichschenkligen, rechtwinkligen usw. Dreiecken zu fragen und den SuS die Möglichkeit zu geben, den Abbildungsbegriff im Kontext von Symmetrien weiter zu vertiefen.
Nachbereitungsauftrag Wibke
Vorteile des abbildungsgeometrischen Ansatzes (nach Bender (1982))
- Universelle mathematische Idee wird vermittelt
- Funktionales Denken wird geschult
- Anschaulichkeit, Dynamik, Selbsttätigkeit
- Strukturverwandtschaft zwischen Abbildungsgruppen und (Denk-)Gruppierungen
- Globale Ordnung
- Lokale Ordnung
- Realitätsbezug
Beispiel
Die folgende SuS-Aktivität ist eine projektorientierte Aufgabe, die sich auch gut als Hausaufgabe stellen lässt. Die SuS sollen Beispiele für Abbildungsgeometrien aus ihrem Alltag sammeln. Dabei sollen die SuS Objekte aus der Umwelt finden, die Achsen- und/oder Punktsymmetrisch sind. Die SuS sollen diese Objekte mitbringen, Bilder davon machen/zeichnen oder eine Beschreibung anfertigen.
Beispiele können Gebäude, Fenster, Brücken, Baupläne, etc. sein.
Nachbereitungsauftrag Katharina
Vorteile des abbildungsgeometrischen Ansatzes
- Abbildungen spielen eine elementare Rolle in der Mathematik
- Verbindung zum Funktionsbegriff
- Dynamischerer Zugang
- Schöne Anwendungsmöglichkeiten bei dynamischer Geometriesoftware
Beispiel
Zur Vertiefung des Themas „Achsenspiegelung“ fertigen SuS Scherenschnitte an und konstruieren somit selbst achsensymmetrische Figuren. In den Scherenschnitten können Winkel- und Längeneigenschaften sowie die Lagebeziehung von Punkten genauer untersucht werden. Anschließend könnte die Lehrperson nur einen Ausschnitt eines Scherenschnittes austeilen, den die SuS in ihr Heft einkleben sollen. Aufgabe soll sein, den Rest der achsensymmetrischen Figur einzuzeichnen.
Nachbereitungsauftrag Anna-Lena
Vorteile des abbildungsgeometrischen Ansatzes
- Verknüpfung des Abbildungsbegriffs mit dem Gruppenbegriff
- Darbietung von handlungsbezogenen Zugängen aufgrund dynamischer Eigenschaft des abbildungsgeometrischen Ansatzes (-> Bewegungsgeometrie + freie Beweglichkeit des starren Körpers)
- Möglichkeit von globalen und lokalen Ordnungsstrukturen (Projektive Geometrie -> Euklidische Geometrie -> Darstellende Geometrie; Invarianzbetrachtungen; beliebige Elementarisierung in Beweisen möglich)
Beispiel
Die SuS sollen regelmäßige geometrische Objekte (gleichseitiges Dreieck, Quadrat, Pentagon, Hexagon, Tetraeder, evtl. Oktaeder, Kegel, Zylinder) auf Spiegelebenen, Dreh- und Drehspiegelachsen enaktiv mit Modellen untersuchen. Durch begleitende Fragestellungen wie
- Welche Operationen/Handlungen können die Figur in eine nicht unterscheidbare Figur überführen, d.h. Eckpunkte auf andere Exkpunkte und Kanten auf Kanten?
- Wie oft muss ich die Operation durchführen, um bei der Usprungsfigur zu landen?
- Ist es möglich Operationen zu einer Operation zusammenzufassen? Wenn ja, welche?
- Was passiert mit den Punkten der einer verkleinerten oder vergrößerten Figur unter der Operation?
- Was passiert mit einem Punkt im Raum der nicht auf der Figur liegt?
- Welche Punkte im Raum/Ebene werden durch die ausgeführte Operation/Handlungen festgehalten?
sollen die SuS enaktiv
- Gruppeneigenschaften von einfachen, meist endlichen Symmetriegruppen erfahren
- den linearen, funktionalen Charakter von geometrischen Abbildungen erfahren
- Invarianten von Drehungen, Spiegelungen und Drehspiegelungen kennenlernen
Es wäre sinnvoll, dass der Lehrer ein Beispiel im Plenum vorführt und die Sus in Gruppen je eine Figur bzw. Körper untersuchen.
Literaturhinweise
- Bender (1982). Abbildungsgeometrie in der didaktischen Diskussion. In Zentralblatt für Didaktik der Mathematik.
- Graumann et al. (1996). Tendenzen der Geometriedidaktik der letzten 20 Jahre. In Journal für Mathematik-Didaktik.
- Filler (2016). Weg von Euklid ⋅ und wieder zurück?. In Mathematische Semesterberichte.
- Kapitel 8 „Symmetrie und Kongruenz“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“.
- Kapitel 9 „Ähnlichkeit“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“.