Lösung von Aufgabe 1.5 (WS 19 20): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie jeweils mit einer Wahrheitstabelle: * <math>(A\Rightarrow B)\Leftrightarrow (\neg A\vee B) </math> * <math>\neg (A \wedge B)</math> <math>\Leftrig…“)
 
 
Zeile 2: Zeile 2:
 
* <math>(A\Rightarrow B)\Leftrightarrow (\neg A\vee B) </math>
 
* <math>(A\Rightarrow B)\Leftrightarrow (\neg A\vee B) </math>
 
* <math>\neg (A \wedge B)</math> <math>\Leftrightarrow</math>  (<math>\neg A</math> <math>\vee </math> <math>\neg B</math>)<br />
 
* <math>\neg (A \wedge B)</math> <math>\Leftrightarrow</math>  (<math>\neg A</math> <math>\vee </math> <math>\neg B</math>)<br />
 +
 +
{| class="wikitable"
 +
|-
 +
! <math>A</math> !! <math>\neg A</math> !! <math>B</math> !! <math>\neg B</math> !! <math>(A\Rightarrow B)</math> !! <math>(\neg A\vee B) </math> !! <math> (A \wedge B)</math> !! <math>\neg (A \wedge B)</math> !! (<math>\neg A</math> <math>\vee </math> <math>\neg B</math>)<br />
 +
|-
 +
|  <math>w</math> || <math>f</math> || <math>f</math> || <math>w</math> || <math>w</math> || <math>w</math> || <math>w</math> || <math>f</math> || <math>f</math>
 +
|-
 +
| <math>w</math> || <math>f</math> || <math>f</math> || <math>w</math> || <math>f</math> || <math>f</math> || <math>f</math> || <math>w</math> || <math>w</math>
 +
|-
 +
| <math>f</math> || <math>w</math> || <math>w</math> || <math>f</math> || <math>w</math> || <math>w</math> || <math>f</math> || <math>w</math> || <math>w</math>
 +
|-
 +
| <math>f</math> || <math>w</math> || <math>w</math> || <math>f</math> || <math>w</math> || <math>w</math> || <math>f</math> || <math>w</math> || <math>w</math>
 +
|}
 +
 +
qed
 +
 +
  
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]

Aktuelle Version vom 14. Oktober 2019, 22:14 Uhr

Beweisen Sie jeweils mit einer Wahrheitstabelle:

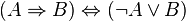
  • (A\Rightarrow B)\Leftrightarrow (\neg A\vee B)
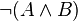
  • \neg (A \wedge B) \Leftrightarrow (\neg A \vee \neg B)
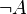
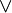
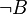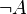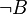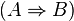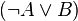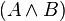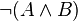A \neg A B \neg B (A\Rightarrow B) (\neg A\vee B) (A \wedge B) \neg (A \wedge B) (\neg A \vee \neg B)
w f f w w w w f f
w f f w f f f w w
f w w f w w f w w
f w w f w w f w w

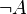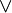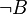qed

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.5_(WS_19_20)&oldid=33738“