Lösung von Aufgabe 5.3 P (WS 19 20): Unterschied zwischen den Versionen
| Zeile 14: | Zeile 14: | ||
Nicht reflexiv: a steht nicht in Relation zu sich selbst <br /> | Nicht reflexiv: a steht nicht in Relation zu sich selbst <br /> | ||
| − | + | transitiv: wenn aRb und bRc dann aRc...bedeutet nicht dass es zwingend vorliegen muss. <br /> | |
Nicht symmetrisch: a steht in Relation zu b aber nicht umgekehrt --[[Benutzer:Emiliam|Emiliam]] ([[Benutzer Diskussion:Emiliam|Diskussion]]) 11:41, 12. Nov. 2019 (CET) | Nicht symmetrisch: a steht in Relation zu b aber nicht umgekehrt --[[Benutzer:Emiliam|Emiliam]] ([[Benutzer Diskussion:Emiliam|Diskussion]]) 11:41, 12. Nov. 2019 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 12. November 2019, 12:05 Uhr
a) Geben Sie die Menge  aller konvexer Drachenvierecke an.
aller konvexer Drachenvierecke an.
M(konvexe Drachenvierecke) = {Drachen; Raute; Quadrat}
--Emiliam (Diskussion) 10:41, 12. Nov. 2019 (CET)
b) Bilden Sie das kartesische Produkt der Menge  .
.
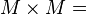 {
{ 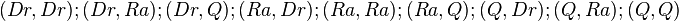 }
}
--Emiliam (Diskussion) 10:41, 12. Nov. 2019 (CET)
c) Wir definineren eine Relation  mit
mit 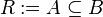 . Bestimmen Sie die Relation
. Bestimmen Sie die Relation  auf
auf  .
.
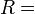 {
{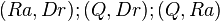 }
}
--Emiliam (Diskussion) 11:22, 12. Nov. 2019 (CET)
d) Untersuchen Sie die Relation  auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
Nicht reflexiv: a steht nicht in Relation zu sich selbst
transitiv: wenn aRb und bRc dann aRc...bedeutet nicht dass es zwingend vorliegen muss.
Nicht symmetrisch: a steht in Relation zu b aber nicht umgekehrt --Emiliam (Diskussion) 11:41, 12. Nov. 2019 (CET)

