Lösung von Aufgabe 1.3 (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 7: | Zeile 7: | ||
- Die Menge 2 und die Menge 3 sind echte Teilmenge von Menge 1.--[[Benutzer:Elisa R.|Elisa R.]] ([[Benutzer Diskussion:Elisa R.|Diskussion]]) 18:52, 18. Apr. 2020 (CEST)<br /> | - Die Menge 2 und die Menge 3 sind echte Teilmenge von Menge 1.--[[Benutzer:Elisa R.|Elisa R.]] ([[Benutzer Diskussion:Elisa R.|Diskussion]]) 18:52, 18. Apr. 2020 (CEST)<br /> | ||
- Die Mengen M_2 und M_3 sind identisch und M_1 ist eine echte Teilmenge von M_2 und M_3. --[[Benutzer:Kohfahlm|Kohfahlm]] ([[Benutzer Diskussion:Kohfahlm|Diskussion]]) 17:26, 22. Apr. 2020 (CEST) | - Die Mengen M_2 und M_3 sind identisch und M_1 ist eine echte Teilmenge von M_2 und M_3. --[[Benutzer:Kohfahlm|Kohfahlm]] ([[Benutzer Diskussion:Kohfahlm|Diskussion]]) 17:26, 22. Apr. 2020 (CEST) | ||
| + | |||
| + | - m2=m3 / m1 teilmenge von m2 und m3--[[Benutzer:Durutti|Durutti]] ([[Benutzer Diskussion:Durutti|Diskussion]]) 15:48, 23. Apr. 2020 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 23. April 2020, 14:48 Uhr
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.
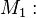Menge aller gleichschenkligen Dreiecke
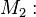Menge aller gleichseitigen Dreiecke
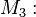Menge aller gleichwinkligen Dreiecke
- Die Menge 2 und die Menge 3 sind identisch.
- Die Menge 2 und die Menge 3 sind echte Teilmenge von Menge 1.--Elisa R. (Diskussion) 18:52, 18. Apr. 2020 (CEST)
- Die Mengen M_2 und M_3 sind identisch und M_1 ist eine echte Teilmenge von M_2 und M_3. --Kohfahlm (Diskussion) 17:26, 22. Apr. 2020 (CEST)
- m2=m3 / m1 teilmenge von m2 und m3--Durutti (Diskussion) 15:48, 23. Apr. 2020 (CEST)
