Der Schwerpunkt und die Seitenhalbierenden eines Dreiecks: Unterschied zwischen den Versionen
(→Definition Seitenhalbierende eines Dreiecks) |
|||
| Zeile 20: | Zeile 20: | ||
Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks ABC und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.<br />--[[Benutzer:Löwenzahn|Löwenzahn]] 10:36, 21. Jul. 2010 (UTC) | Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks ABC und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.<br />--[[Benutzer:Löwenzahn|Löwenzahn]] 10:36, 21. Jul. 2010 (UTC) | ||
| − | + | ==== Satz: Existenz und Eindeutigkeit der Seitenhalbierende ==== | |
| + | ===== Teil 1: Existenz ===== | ||
| + | Voraussetzung: Dreieck <math>\overline{ABC}</math> mit schulüblichen Bezeichnungen | ||
| + | <br />Behauptung: (o.B.d.A) Es existiert eine Gerade <math>\ s_a</math> zwischen dem Mittelpunkt der Seite <math>\ a</math> und dem Punkt <math>\ A</math>. | ||
| + | ::(1) Es existiert (genau) ein Punkt <math>\ M_a</math>: Mittelpunkt der Seite a (der Strecke <math>\overline {BC}</math>). | ||
| + | :::Begründung - Satz III.1: (Existenz '''und Eindeutigkeit''' des Mittelpunkte einer Strecke) | ||
| + | ::(2) Es existiert (genau) eine Gerade <math>\ s_a</math>, die durch die Punkte <math>\ M_a</math> und <math>\ A</math> geht. | ||
| + | :::Begründung - Axiom I.1: (Axiom von der Geraden) "Zu zwei beliebigen verschiedenen Punkten gibt es '''genau''' eine Gerade, die die beiden Punkte enthält. " | ||
| + | |||
| + | ===== Teil 2: Eindeutigkeit===== | ||
| + | Da die in Schritt (1) und (2) verwandten Sätze / Axiome von Existenz '''und Eindeutigkeit''' sprechen, ist mit obigen Existenz-"Beweis" auch die Eindeutigkeit bewiesen. --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 15:32, 21. Jul. 2010 (UTC) | ||
== Schwerpunkt eines Dreiecks == | == Schwerpunkt eines Dreiecks == | ||
Version vom 21. Juli 2010, 16:32 Uhr
Die Fotos demonstrieren, was unter dem Schwerpunkt eines Dreiecks zu verstehen ist. Erstellen Sie das Skript selbst.
|
|
|---|---|
|
|
|
|
Inhaltsverzeichnis |
Seitenhalbierende eines Dreiecks
Definition Seitenhalbierende eines Dreiecks
Eine Seitenhalbierende eines Dreiecks ist eine Gerade die durch einen Eckpunkt des Dreiecks ABC und den Mittelpunkt der gegenüberliegenden Seite dieses Eckpunktes verläuft.
--Löwenzahn 10:36, 21. Jul. 2010 (UTC)
Satz: Existenz und Eindeutigkeit der Seitenhalbierende
Teil 1: Existenz
Voraussetzung: Dreieck 
mit schulüblichen Bezeichnungen
Behauptung: (o.B.d.A) Es existiert eine Gerade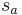 
zwischen dem Mittelpunkt der Seite 
und dem Punkt 
.
- (1) Es existiert (genau) ein Punkt
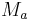: Mittelpunkt der Seite a (der Strecke 
).
- Begründung - Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- (2) Es existiert (genau) eine Gerade 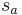, die durch die Punkte 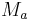und geht.
- Begründung - Axiom I.1: (Axiom von der Geraden) "Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält. "
- (1) Es existiert (genau) ein Punkt
Teil 2: Eindeutigkeit
Da die in Schritt (1) und (2) verwandten Sätze / Axiome von Existenz und Eindeutigkeit sprechen, ist mit obigen Existenz-"Beweis" auch die Eindeutigkeit bewiesen. --Heinzvaneugen 15:32, 21. Jul. 2010 (UTC)
Schwerpunkt eines Dreiecks
Satz: Schnittpunkt der Seitenhalbierende eines Dreiecks
Die Seitenhalbierenden eines Dreiecks schneiden sich in (genau?) einem Punkt.
--Löwenzahn 10:37, 21. Jul. 2010 (UTC)
Definition Schwerpunkt eines Dreiecks
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der Seitenhalbierenden des Dreiecks.--Löwenzahn 10:36, 21. Jul. 2010 (UTC)
