Lösung von Aufg. 6.3P (SoSe 20): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 41: Zeile 41:
 
  Außerdem wäre es super, wenn du immer die "alten" Sachen stehen lässt und das Verbesserte unter die Kommentare  
 
  Außerdem wäre es super, wenn du immer die "alten" Sachen stehen lässt und das Verbesserte unter die Kommentare  
 
  schreiben würdest. Danke.  --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 21:38, 28. Mai 2020 (CEST)
 
  schreiben würdest. Danke.  --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 21:38, 28. Mai 2020 (CEST)
 +
 +
Voraussetzung: zwei konvexe Punktmengen
 +
 +
Behauptung: Durchschnitt dieser Mengen ist konvex
 +
 +
Zusatz: Es seien die Punkte A und B, mit <math>(A,B \epsilon M \cap N)</math>.
 +
 +
{| class="wikitable"
 +
|-
 +
!  || Beweisschritt !! Begründung
 +
|-
 +
| 1) || <math>(A,B \epsilon M,N)</math> || Zusatz
 +
|-
 +
| 3) || <math>(\overline {AB} \subseteq M)</math> || 1), Voraussetzung
 +
|-
 +
| 4) || <math>(\overline {AB} \subseteq N)</math> || 1), Voraussetzung
 +
|-
 +
| 5) || <math>(\overline {AB} \subseteq M \cap N)</math> || 3), 4)
 +
|-
 +
| 6) || <math>(M \cap N)</math> ist konvex || 4), Definition konvex
 +
|}
 +
--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]])
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]

Version vom 8. Juni 2020, 16:47 Uhr

Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.


Voraussetzung: zwei konvexe Punktmengen

Behauptung: Durchschnitt dieser Mengen ist konvex

Zusatz: Es seien die Punkte A und B, mit 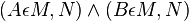(A \epsilon M,N) \wedge (B \epsilon M,N).

Beweisschritt Begründung
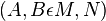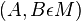1) (A,B \epsilon M,N) Zusatz
2) (A,B \epsilon M) 1)
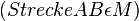3) (Strecke AB \epsilon M) 2), Voraussetzung
4) 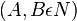(A,B \epsilon N) 1)
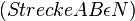5) (Strecke AB \epsilon N) 4), Voraussetzung
6) 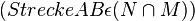(Strecke AB \epsilon (N \cap M)) 3), 5)
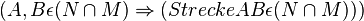7) (A,B \epsilon (N \cap M)\Rightarrow (Strecke AB \epsilon (N \cap M))) 1)-6) (Zusammenfassung der Folgerungen)
8) 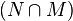(N \cap M) ist konvex 7), Definition konvex

--tgksope (Diskussion) 

Grundsätzlich ist der Beweis (mit ein paar kleinen Ausnahmen) richtig geführt, 
nur etwas zu umständlich.
Als ersten Schritt bestimmst du, dass A und B zwei beliebige Punkte in M \cap N seien.
Dann musst du beachten, dass  \overline {AB} \in N nicht korrekt ist. 
Ein Element ist immer ein einzelnes Objekt einer Menge. Hier hast du eine Strecke
mit mehreren Elementen. Da heißt es dann immer  \overline {AB}   ist Teilmenge von N. ( \overline {AB}  \subseteq N )
Nachdem du bewiesen hast, dass  \overline {AB}   Teilmenge von M und N ist, 
reicht es zu sagen, dass  \overline {AB}  \subseteq M \cap N). Damit ist bewiesen, dass  M \cap N 
konvex ist. Vielleicht kannst du den Beweis erneut führen.
Außerdem wäre es super, wenn du immer die "alten" Sachen stehen lässt und das Verbesserte unter die Kommentare 
schreiben würdest. Danke.  --Tutorin Laura (Diskussion) 21:38, 28. Mai 2020 (CEST)

Voraussetzung: zwei konvexe Punktmengen

Behauptung: Durchschnitt dieser Mengen ist konvex

Zusatz: Es seien die Punkte A und B, mit 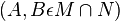(A,B \epsilon M \cap N).

Beweisschritt Begründung
1) 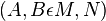(A,B \epsilon M,N) Zusatz
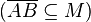3) (\overline {AB} \subseteq M) 1), Voraussetzung
4) 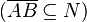(\overline {AB} \subseteq N) 1), Voraussetzung
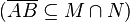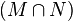5) (\overline {AB} \subseteq M \cap N) 3), 4)
6) (M \cap N) ist konvex 4), Definition konvex

--tgksope (Diskussion)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._6.3P_(SoSe_20)&oldid=35514“