Lösung von Aufg. 7.4P (SoSe 20): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Wir gehen von folgender Definition aus: Ein rechter Winkel ist ein Winkel, der das gleiche Maß wie einer seiner Nebenwinkel hat. Außerdem gelte Satz IV.2: Ne…“)
 
Zeile 4: Zeile 4:
  
  
 +
Voraussetzung: rechter Winkel
  
 +
Behauptung: Maß 90
 +
 +
Zusatz: Es sei <math> \alpha</math> ein rechter Winkel und <math> \beta</math> ein Nebenwinkel von <math> \alpha</math>.
 +
 +
{| class="wikitable"
 +
|-
 +
!  || Beweisschritt !! Begründung
 +
|-
 +
| 1) || <math>\alpha = \beta</math> || Voraussetzung, Zusatz, Def. rechter Winkel
 +
|-
 +
| 2) || <math>\alpha+\beta=180</math> || Zusatz, Def. Nebenwinkel
 +
|-
 +
| 3) || <math>\alpha=90</math> || 1), 2)
 +
|}
 +
--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]])
  
  
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]

Version vom 8. Juni 2020, 17:11 Uhr

Wir gehen von folgender Definition aus: Ein rechter Winkel ist ein Winkel, der das gleiche Maß wie einer seiner Nebenwinkel hat. Außerdem gelte Satz IV.2: Nebenwinkel sind supplementär. Beweisen Sie: Jeder rechte Winkel hat das Maß 90.


Voraussetzung: rechter Winkel

Behauptung: Maß 90

Zusatz: Es sei \alpha ein rechter Winkel und \beta ein Nebenwinkel von \alpha.

Beweisschritt Begründung
1) 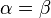\alpha = \beta Voraussetzung, Zusatz, Def. rechter Winkel
2) 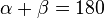\alpha+\beta=180 Zusatz, Def. Nebenwinkel
3) 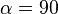\alpha=90 1), 2)

--tgksope (Diskussion)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._7.4P_(SoSe_20)&oldid=35516“