Lösung von Aufg. 7.4P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 28: | Zeile 28: | ||
Zwischen deinem 2) und 3) Schritt kannst du noch die Rechnung einfügen. | Zwischen deinem 2) und 3) Schritt kannst du noch die Rechnung einfügen. | ||
Tipp: aus <math>\mid\alpha\mid + \mid\beta\mid wird \mid\alpha\mid+\mid\alpha\mid </math> | Tipp: aus <math>\mid\alpha\mid + \mid\beta\mid wird \mid\alpha\mid+\mid\alpha\mid </math> | ||
| − | Der Beweis kann so beginnen: | + | Der Beweis kann so beginnen: --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 12:06, 9. Jun. 2020 (CEST) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
Version vom 9. Juni 2020, 11:06 Uhr
Wir gehen von folgender Definition aus: Ein rechter Winkel ist ein Winkel, der das gleiche Maß wie einer seiner Nebenwinkel hat. Außerdem gelte Satz IV.2: Nebenwinkel sind supplementär.
Beweisen Sie: Jeder rechte Winkel hat das Maß 90.
Voraussetzung: rechter Winkel
Behauptung: Maß 90
Zusatz: Es sei  ein rechter Winkel und
ein rechter Winkel und  ein Nebenwinkel von
ein Nebenwinkel von  .
.
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 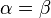 |
Voraussetzung, Zusatz, Def. rechter Winkel |
| 2) | 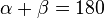 |
Zusatz, Def. Nebenwinkel |
| 3) | 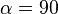 |
1), 2) |
--tgksope (Diskussion)
Zuerst musst du bei den Winkeln immerschreiben, d.h. an die Striche denken, wenn es um das konkrete Maß geht. Die Zusätze kannst du auch direkt in die Beweise mit einfügen. Zwischen deinem 2) und 3) Schritt kannst du noch die Rechnung einfügen. Tipp: aus
Der Beweis kann so beginnen: --Tutorin Laura (Diskussion) 12:06, 9. Jun. 2020 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) |  sei Nebenwinkel von sei Nebenwinkel von  |
Zu jedem Winkel lässt sich ein Nebenwinkel konstruieren. |
| 2) |  hat das gleiche Maß wie hat das gleiche Maß wie  |
Vor., 1), Def. rechter Winkel |
| 3) | ... | ... |

