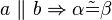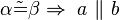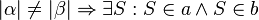Lösung von Aufgabe 4.3 (SoSe 20): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch e…“)
 
Zeile 6: Zeile 6:
 
#<math>\ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta </math>
 
#<math>\ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta </math>
  
−
 
+
#äquivalent, da genau der Stufenwinkelsatz dargestellt wurde
 +
#wahr, aber nicht äquivalent zu Stufenwinkelsatz, weil es die Umkehrung davon ist
 +
#äquivalent, da es die Kontraposition des Stufenwinkelsatzes darstellt
 +
#wahr, aber nicht äquivalent, da die Umkehrung enthalten ist
 +
--[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 15:55, 19. Jul. 2020 (CEST)
  
  

Version vom 19. Juli 2020, 14:55 Uhr

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel \alpha und \beta . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?

  1. \ a \ \| \ b \Rightarrow \alpha \tilde {=} \beta
  2. \alpha \tilde {=} \beta \Rightarrow \ a \ \| \ b
  3. \left|\alpha \right|\not= \left| \beta \right| \Rightarrow \exists S: S \in a \wedge S \in b
  4. \ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta
  1. äquivalent, da genau der Stufenwinkelsatz dargestellt wurde
  2. wahr, aber nicht äquivalent zu Stufenwinkelsatz, weil es die Umkehrung davon ist
  3. äquivalent, da es die Kontraposition des Stufenwinkelsatzes darstellt
  4. wahr, aber nicht äquivalent, da die Umkehrung enthalten ist

--tgksope (Diskussion) 15:55, 19. Jul. 2020 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_4.3_(SoSe_20)&oldid=35966“