Lösung von Aufgabe 11.4P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Durch welche Abbildung kann die Verkettung zweier Punktspiegelungen ersetzt werden? Begründen Sie! <br /> Kategorie:Geo_P“) |
|||
| Zeile 3: | Zeile 3: | ||
| − | + | Durch eine Verschiebung: Ich kann bei <math>S_a\circ S_b \circ S_c\circ S_d</math> (mit <math>S_a\circ S_b</math> und <math>S_c\circ S_d</math> sind jeweils Punktspiegelungen) die Geraden a und b um ihren Schnittpunkt S so drehen, dass b durch den Schnittpunkt M von c und d geht. Nun drehe ich c und d um M, bis c auf b zu liegen kommt. Durch die Hintereinander-Ausführung der Spiegelungen an b und c mit b=c, fallen b und c als Spiegelachsen weg. Durch die Drehungen gilt: a parallel zu d, womit wir eine Verschiebung <math>S_a\circ S_d</math> erhalten. --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 11:38, 25. Jul. 2020 (CEST) | |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 25. Juli 2020, 10:38 Uhr
Durch welche Abbildung kann die Verkettung zweier Punktspiegelungen ersetzt werden? Begründen Sie!
Durch eine Verschiebung: Ich kann bei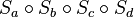 
(mit 
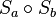und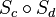 
sind jeweils Punktspiegelungen) die Geraden a und b um ihren Schnittpunkt S so drehen, dass b durch den Schnittpunkt M von c und d geht. Nun drehe ich c und d um M, bis c auf b zu liegen kommt. Durch die Hintereinander-Ausführung der Spiegelungen an b und c mit b=c, fallen b und c als Spiegelachsen weg. Durch die Drehungen gilt: a parallel zu d, womit wir eine Verschiebung 
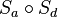erhalten. --tgksope (Diskussion) 11:38, 25. Jul. 2020 (CEST)
