Benutzer:Dwight Kurt Schrute: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 5: | Zeile 5: | ||
'''Volumen:''' | '''Volumen:''' | ||
| − | Da die Grundfläche, eines Zylinders, ein Kreis ist, gilt <math>G= \pi r^{2}</math>, wobei '''r''' der Radius der Grundfläche ist. | + | Da die Grundfläche, eines Zylinders, ein Kreis ist, gilt <math>G= \pi r^{2}</math> , wobei '''r''' der Radius der Grundfläche ist. |
| − | Damit ergibt sich: | + | Damit ergibt sich: <math>V = \pi r^{2}h</math> |
In meinem Fall wäre also das Volumen des Stiftebechers ungefähr '''636cm<sup>3</sup>'''. | In meinem Fall wäre also das Volumen des Stiftebechers ungefähr '''636cm<sup>3</sup>'''. | ||
| Zeile 15: | Zeile 15: | ||
Um die Oberfläche zu berechnen brauchen wir wieder den Radius, sowie die Höhe. | Um die Oberfläche zu berechnen brauchen wir wieder den Radius, sowie die Höhe. | ||
| − | Die Formel sieht wie folgt aus: | + | Die Formel sieht wie folgt aus: A=2 \pi r(r+h) |
Somit wäre die Oberfläche '''410cm<sup>2</sup>'''. | Somit wäre die Oberfläche '''410cm<sup>2</sup>'''. | ||
| − | Jedoch muss noch einmal die Grundfläche G abgezogen werden, da der Zylinder nach obenhin geöffnet ist ( | + | Jedoch muss noch einmal die Grundfläche G abgezogen werden, da der Zylinder nach obenhin geöffnet ist (<math>G= \pi r^{2}</math>). |
Damit ergibt sich eine ungefähre Fläche von '''346cm<sup>2</sup>'''. | Damit ergibt sich eine ungefähre Fläche von '''346cm<sup>2</sup>'''. | ||
| − | |||
| − | |||
--[[Benutzer:Dwight Kurt Schrute|Dwight Kurt Schrute]] ([[Benutzer Diskussion:Dwight Kurt Schrute|Diskussion]]) 11:29, 3. Nov. 2020 (CET) | --[[Benutzer:Dwight Kurt Schrute|Dwight Kurt Schrute]] ([[Benutzer Diskussion:Dwight Kurt Schrute|Diskussion]]) 11:29, 3. Nov. 2020 (CET) | ||
Version vom 3. November 2020, 12:13 Uhr
Die Maße des Zylinders sind h = 10 und r = 4,5
Volumen:
Da die Grundfläche, eines Zylinders, ein Kreis ist, gilt 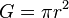 , wobei r der Radius der Grundfläche ist.
, wobei r der Radius der Grundfläche ist.
Damit ergibt sich: 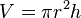
In meinem Fall wäre also das Volumen des Stiftebechers ungefähr 636cm3.
Oberfläche:
Um die Oberfläche zu berechnen brauchen wir wieder den Radius, sowie die Höhe.
Die Formel sieht wie folgt aus: A=2 \pi r(r+h)
Somit wäre die Oberfläche 410cm2.
Jedoch muss noch einmal die Grundfläche G abgezogen werden, da der Zylinder nach obenhin geöffnet ist (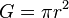 ).
).
Damit ergibt sich eine ungefähre Fläche von 346cm2.
--Dwight Kurt Schrute (Diskussion) 11:29, 3. Nov. 2020 (CET)


