Beweise von Studenten: Unterschied zwischen den Versionen
(→Umkehrung des Satz des Thales) |
|||
| Zeile 134: | Zeile 134: | ||
::Es gilt (nach VSS)<math>\overline{M_CA} \cong \overline{M_cB}</math>. | ::Es gilt (nach VSS)<math>\overline{M_CA} \cong \overline{M_cB}</math>. | ||
::Wenn <math>\overline{M_cA} \cong \overline{M_cB} \cong \overline{M_cC}</math>, liegt <math>\ C</math> auf dem Kreis <math>\ k</math>. | ::Wenn <math>\overline{M_cA} \cong \overline{M_cB} \cong \overline{M_cC}</math>, liegt <math>\ C</math> auf dem Kreis <math>\ k</math>. | ||
| − | + | Lemma und Behauptung sind äquivalente Aussagen: trivial - wenn <math>\ C</math> zu <math>\ M_c</math> den selben Abstand hat wie (zB) <math>\ A</math> zu <math>\ M_c</math>, dann liegt <math>\ C</math> mit <math>\ A</math> auf dem selben Kreis <math>\ k</math> um <math>\ M_c</math>. | |
| − | Weiterhin gehe ich von einer Hilfskonstruktion aus, die im Applet dargestellt wird. | + | Weiterhin gehe ich von einer Hilfskonstruktion aus, die im Applet dargestellt wird. |
# VSS: Dreieck <math>\overline {ABC}</math>, <math>\ |\gamma| = </math>90, <math>\ M_c</math> | # VSS: Dreieck <math>\overline {ABC}</math>, <math>\ |\gamma| = </math>90, <math>\ M_c</math> | ||
# BEH: <math>\ C</math> liegt auf Kreis <math>\ k</math> | # BEH: <math>\ C</math> liegt auf Kreis <math>\ k</math> | ||
# Parallele zu <math>\overline{AB}</math> durch <math>\ C</math> | # Parallele zu <math>\overline{AB}</math> durch <math>\ C</math> | ||
| − | # Parallele zu <math>\overline{ | + | # Parallele zu <math>\overline{CM_c}</math> durch <math>\ B</math> |
| − | # ohne Beweise auszuführen | + | # ohne Beweise auszuführen stellt man fest: <math>\gamma_1 \cong \gamma'_1</math> (<math>\angle M_cCB \cong \angle M_c'BC</math>: Wechselwinkel an Parallelen) |
| − | # | + | # ...<math>\beta \cong \beta'</math> (<math>\angle CBM_c \cong \angle BCM_c'</math>: Wechselwinkel an Parallelen) |
| + | # ...<math>\epsilon_1 \cong \epsilon'_1</math> und <math>\epsilon_2 \cong \epsilon'_2</math> (Wechselwinkel an Parallelen) | ||
| + | # ...<math>\delta_1 \cong \delta_2</math> (Scheitelwinkel) | ||
| + | |||
| + | Nach dieser Leichtigkeit nun der eigentliche Beweis: | ||
| + | {| class="wikitable" | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VI) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VII) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VIII) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IX) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(X) | ||
| + | | | ||
| + | | | ||
| + | |} | ||
Version vom 24. Juli 2010, 00:21 Uhr
Inhaltsverzeichnis |
Satz: Wenn ein Viereck ein Rechteck...
Wenn ein Viereck ein Rechteck ist, dann sind seine Diagonalen gleich lang und sie halbieren sich.
- Idee: Man muss dabei ja 1. die gleichlangen Diagonalen und 2. die sich halbierenden Diagonalen zeigen. Habe aber einfach ein Problem den Beweis zu den gleichlangen Diagonalen zu führen. Hat jemand eine Idee?--Löwenzahn 15:52, 20. Jul. 2010 (UTC)
Geht das nicht über SWS? Also wenn du das Rechteck ABCD hast, z.B. die beiden Dreiecke ABD und ABC vergleichen, die müssten laut SWS kongruent sein, damit also auch die Diagonalen. --Ncesi1 15:57, 20. Jul. 2010 (UTC)
Kann ich denn in einem Rechteck davon ausgehen, dass wir einen rechten Winkel bei 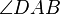 und
und 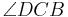 haben? Dann würde SWS gehen, das würde ich dann verstehen...--Löwenzahn 16:11, 20. Jul. 2010 (UTC)
haben? Dann würde SWS gehen, das würde ich dann verstehen...--Löwenzahn 16:11, 20. Jul. 2010 (UTC)
Davon kann man natürlich ausgehen, das ist schließlich eins der Merkmale von Rechtecken. Die Kombination der Dreiecke DAB und DCB würde dir aber, wenn ich richtig liege, nicht weiterhelfen, weil du dann nur eine der beiden Diagonalen betrachtest. Du musst also die Dreiecke so wählen, dass beide Diagonalen betrachtet werden (z.B. ABD und ABC). --Ncesi1 16:15, 20. Jul. 2010 (UTC)
Ah, ok, danke... sonst müsste man den Beweis ja doppelt führen, oder? Insofern ist es wirklich logischer. Blöde Frage, aber wir müssen Rechteck immer über die Innenwinkel definieren, oder geht es auch anders? Sonst müsste man vor dem Beweis sich ja für eine Art Definition entscheiden?!?!?! Und müsste man nicht sogar noch zeigen, dass alle Winkel = 90 sind?!?! Nach Def (Ein Viereck mit zwei Paar parallelen Seiten und einem rechten Innenwinkel ist ein Rechteck) benötigt man ja nur einen...--Löwenzahn 16:19, 20. Jul. 2010 (UTC)
Ich weiß nicht, ob man das alles in diesen Beweis mit reinschreiben müsste, oder ob man einfach alles als gegeben nehmen kann. Über die Definition mit dem einen rechten Innenwinkel kommt man doch mit Hilfe der Stufenwinkel etc. darauf, dass alle Winkel rechte Winkel sind, oder? --Ncesi1 16:27, 20. Jul. 2010 (UTC)
Denke auch, dass man über Stufen- und Scheitelwinkelsatz und Supplementaxiom zeigen kann, dass alle Winkel = 90 sind. Aber dann müsste es doch klappen... oder?
--Löwenzahn 16:37, 20. Jul. 2010 (UTC)
Ich denke auch, dass man spätestens damit dann auf der ganz sicheren Seite wäre. --Ncesi1 16:38, 20. Jul. 2010 (UTC)
Super... danke dir :-)-- 17:30, 20. Jul. 2010 (UTC)
Kann ich auch einfach davon ausgehen, dass die gegenüberliegenden Seiten gleichlang sind, eigentlich schon oder?
Ich würde sagen, dass ist durch die Definition Rechteck gewährleistet.--Löwenzahn 08:58, 21. Jul. 2010 (UTC)
Satz: Umkehrung entgegengesetzt liegender Winkel
Sind entgegengesetzt liegende Winkel an geschnittenen Geraden suplementär, so sind die Geraden parallel.
VSS: c schneidet a und c schneidet b, oBdA  und
und 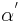 sind entgegengesetzt liegende Winkel,
sind entgegengesetzt liegende Winkel, 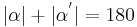
Beh: 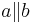
ANN: 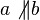 --> es existiert ein Punkt S, der in der Schnittmenge von a und b liegt.
--> es existiert ein Punkt S, der in der Schnittmenge von a und b liegt.
Müsste man hier nicht die beiden Fälle unterscheiden, für die es sich um entgegengesetzt liegende Winkel handelt?
1. Der Schnitt der Schenkel der Winkel, die Teilmenge ein und derselben Geraden sind, ist die leere Menge.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 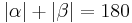 --> --> 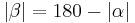
|
(Def. Nebenwinkel), (Supplementaxiom), (rechnen mit reellen Zahlen) |
| (II) | 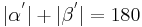 --> --> 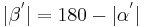
|
(Def. Nebenwinkel), (Supplementaxiom), (rechnen mit reellen Zahlen) |
| (III) | 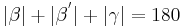
|
(Innenwinkelsumme im Dreieck) |
| (IV) | 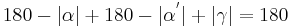
|
(I), (II), (III), (rechnen mit reellen Zahlen) |
| (V) | 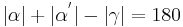
|
(IV), (rechnen mit reellen Zahlen) |
| (VI) | da nach VSS gilt 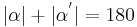 , folgt daraus dass , folgt daraus dass 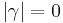 , wodurch die Geraden identisch wären, was in Widerspruch zur Existenz der entgegengesetzt liegenden Winkel ist. Außerdem gibt es keine Nullwinkel oder gestreckte Winkel --> ANN falsch --> Beh gilt , wodurch die Geraden identisch wären, was in Widerspruch zur Existenz der entgegengesetzt liegenden Winkel ist. Außerdem gibt es keine Nullwinkel oder gestreckte Winkel --> ANN falsch --> Beh gilt
|
2. Die Schnittmenge der Schenkel der Winkel, die Teilmenge ein und derselben Geraden sind, bildet eine Strecke.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 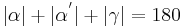
|
(Innenwinkelsumme im Dreieck) |
| (II) | da nach VSS gilt 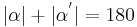 , folgt daraus dass , folgt daraus dass 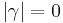 , wodurch die Geraden identisch wären, was in Widerspruch zur Existenz der entgegengesetzt liegenden Winkel ist. Außerdem gibt es keine Nullwinkel oder gestreckte Winkel --> ANN falsch --> Beh gilt , wodurch die Geraden identisch wären, was in Widerspruch zur Existenz der entgegengesetzt liegenden Winkel ist. Außerdem gibt es keine Nullwinkel oder gestreckte Winkel --> ANN falsch --> Beh gilt
|
Was haltet ihr davon? Waren uns in der Lerngruppe so unsicher, ob das so in Ordnung ist.
--Löwenzahn 17:56, 20. Jul. 2010 (UTC)
Meinen Berechnungen zufolge wäre 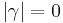 , was kein Widerspruch zum Winkelmaßaxiom wäre. Ihr könntet aber daraus folgern dass die beiden Geraden identisch sein müssen und dies ist Widerspruch zur Voraussetzung (= die Existenz der entgegengesetzten Winkel)--Principella 20:44, 20. Jul. 2010 (UTC)
, was kein Widerspruch zum Winkelmaßaxiom wäre. Ihr könntet aber daraus folgern dass die beiden Geraden identisch sein müssen und dies ist Widerspruch zur Voraussetzung (= die Existenz der entgegengesetzten Winkel)--Principella 20:44, 20. Jul. 2010 (UTC)
Ich würde auch sagen, dass 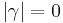 , jedoch wäre das für mich schon ein Widerspruch, da es bei uns weder Nullwinkel, noch gestreckte Winkel gibt. Habe außerdem den Beweis in 4 Fälle aufgeteilt (für jede mögliche Lage, wobei jeweils 2 fast analog ablaufen wegen Scheitelwinkel etc). Würden die beiden Fälle oben reichen?--"chris"07 08:47, 21. Jul. 2010 (UTC)
, jedoch wäre das für mich schon ein Widerspruch, da es bei uns weder Nullwinkel, noch gestreckte Winkel gibt. Habe außerdem den Beweis in 4 Fälle aufgeteilt (für jede mögliche Lage, wobei jeweils 2 fast analog ablaufen wegen Scheitelwinkel etc). Würden die beiden Fälle oben reichen?--"chris"07 08:47, 21. Jul. 2010 (UTC)
Stimmt... 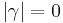 , ich finde auch beide Argumentationen gut---> habe es oben in der Tabelle verbessert. @"chris"07, welche beiden Fälle hast du denn noch unterschieden?--Löwenzahn 08:57, 21. Jul. 2010 (UTC)
, ich finde auch beide Argumentationen gut---> habe es oben in der Tabelle verbessert. @"chris"07, welche beiden Fälle hast du denn noch unterschieden?--Löwenzahn 08:57, 21. Jul. 2010 (UTC)
Trapez ist Sehnenviereck
Stimmt folgender Satz:
"Ein Trapez ist genau dann gleichschenklig, wenn es ein Sehnenviereck ist"?
Das würde doch die Implikation und Umkehrung enthalten (also Äquivalenz, bzw. Kriterium):
- Wenn ein Trapez gleichschenklig ist, dann ist es ein Sehnenviereck.
- Wenn ein Trapez ein Sehnenviereck ist, dann ist es gleichschenklig.
Stimmt die Formulierung??--Löwenzahn 15:43, 23. Jul. 2010 (UTC)
Re: --Heinzvaneugen 20:30, 23. Jul. 2010 (UTC)
- Die Formulierung der Implikationen stimmen:
- Aussage
 (VSS): Gleichschenkliges Trapez
(VSS): Gleichschenkliges Trapez
- Aussage
 (Beh.): Ein Trapez mit Umkreis / Das Trapez ist ein Sehnenviereck.
(Beh.): Ein Trapez mit Umkreis / Das Trapez ist ein Sehnenviereck.
- Implikation (Hin)
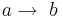 : Wenn Trapez gleichschenklig, dann ist das Trapez ein Sehnenviereck.
: Wenn Trapez gleichschenklig, dann ist das Trapez ein Sehnenviereck.
- Implikation (Rück)
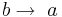 : Wenn ein Trapez ein Sehnenviereck ist, dann ist es gleichschenklig.
: Wenn ein Trapez ein Sehnenviereck ist, dann ist es gleichschenklig.
- Implikation (Hin)
- Aus der total bescheuert klingenden Aussage
 kann man den "Fehler" der Äquivalenz entdecken.
kann man den "Fehler" der Äquivalenz entdecken.
- Äquivalenz
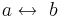 Genau dann, wenn ein Trapez gleichschenklig ist, ist das Trapez ein Sehnenviereck.
Genau dann, wenn ein Trapez gleichschenklig ist, ist das Trapez ein Sehnenviereck.
- Warum so kleinlich? Die "Rück"-Richtung der oberen Äquivalenz wäre (genau genommen): Wenn ein Sehnenviereck, dann gleichschenkliges Trapez.
- Es muss also (zB durch copy und paste) die Aussage
 und die Aussage
und die Aussage  beliebig austauschbar sein. Wenn also das "es" im Satz durch "das Trapez" ersetzt wird, ist man ausm Schneider.
beliebig austauschbar sein. Wenn also das "es" im Satz durch "das Trapez" ersetzt wird, ist man ausm Schneider.
- Äquivalenz
- Das gilt es zu beweisen....
Umkehrung des Satz des Thales
Nur als kleine Anmerkung vorneweg: Sorry an alle, denen ich sagte, dass es doch totaaal einfach wäre, von wegen über Innenwinkelsumme der Dreiecke usw. So einfach geht es leider nicht. Aber ich habe eine Lösung gefunden, die nicht über Widerspruchsbeweis und den Zusammenhang Seitenlänge und Größe des gegenüber liegenden Winkels den Beweis führt. Im Nachhinein (echt!) habe ich den Ansatz auch im Geowiki gefunden...
Satz des Thales
Es sei  ein Kreis mit einem Durchmesser
ein Kreis mit einem Durchmesser  . Jeder Peripheriewinkel von
. Jeder Peripheriewinkel von  über
über  ist ein rechter Winkel.
ist ein rechter Winkel.
Hier kann man sich prima Illustrationen ansehen.
Umkehrung des Satz des Thales
Wenn in einem Dreieck  ein Innenwinkel ein rechter Winkel ist, so liegt der Scheitelpunkt dieses Innenwinkels auf einem Kreis
ein Innenwinkel ein rechter Winkel ist, so liegt der Scheitelpunkt dieses Innenwinkels auf einem Kreis  , wobei die gegenüberliegende Dreiecksseite ein Durchmesser des Kreises
, wobei die gegenüberliegende Dreiecksseite ein Durchmesser des Kreises  ist.
ist.
- Stimmt die Umkehrung so? Kompliziert aber zweckmäßig, oder?
Voraussetzung:
- Dreieck
 mit schulüblichen Bezeichnungen
mit schulüblichen Bezeichnungen
- (oBdA)
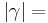 90
90
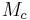 ist der Mittelpunkt von
ist der Mittelpunkt von 
- Kreis
 sei der Kreis mit dem Mittelpunkt
sei der Kreis mit dem Mittelpunkt 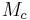 ,
,  sei ein Durchmesser von
sei ein Durchmesser von 
- Dreieck
Behauptung:
 liegt auf Kreis
liegt auf Kreis 
Soweit ist die Umkehrung noch zur erkennen. Um die Skizze verständlich zu machen (und den Beweis zu verkürzen), gehe ich von einem Lemma aus, das besagt:
- Es gilt (nach VSS)
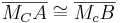 .
.
- Wenn
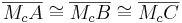 , liegt
, liegt  auf dem Kreis
auf dem Kreis  .
.
- Es gilt (nach VSS)
Lemma und Behauptung sind äquivalente Aussagen: trivial - wenn  zu
zu 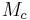 den selben Abstand hat wie (zB)
den selben Abstand hat wie (zB)  zu
zu 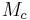 , dann liegt
, dann liegt  mit
mit  auf dem selben Kreis
auf dem selben Kreis  um
um 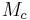 .
.
Weiterhin gehe ich von einer Hilfskonstruktion aus, die im Applet dargestellt wird.
- VSS: Dreieck
 ,
, 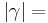 90,
90, 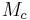
- BEH:
 liegt auf Kreis
liegt auf Kreis 
- Parallele zu
 durch
durch 
- Parallele zu
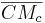 durch
durch 
- ohne Beweise auszuführen stellt man fest:
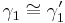 (
(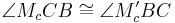 : Wechselwinkel an Parallelen)
: Wechselwinkel an Parallelen)
- ...
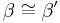 (
(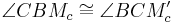 : Wechselwinkel an Parallelen)
: Wechselwinkel an Parallelen)
- ...
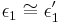 und
und 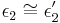 (Wechselwinkel an Parallelen)
(Wechselwinkel an Parallelen)
- ...
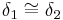 (Scheitelwinkel)
(Scheitelwinkel)
Nach dieser Leichtigkeit nun der eigentliche Beweis:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | ||
| (II) | ||
| (III) | ||
| (IV) | ||
| (V) | ||
| (VI) | ||
| (VII) | ||
| (VIII) | ||
| (IX) | ||
| (X) |

