Verkettung von drei Geradenspiegelungen WS 20 21: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „=== Verkettung von drei Geradenspiegelungen === Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei…“) |
|||
| Zeile 19: | Zeile 19: | ||
Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.<br /> | Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.<br /> | ||
Beweis:<br /><br /> | Beweis:<br /><br /> | ||
| + | |||
| + | [[Category:Geo_P]] | ||
Aktuelle Version vom 21. Januar 2021, 11:10 Uhr
Inhaltsverzeichnis |
Verkettung von drei Geradenspiegelungen
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Geradenspiegelungen? (gerne auch als Bild).
Satz X.1:
- Die Verkettung von drei Geradenspiegelungen
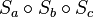an zueinander parallelen Geraden a, b und c ist eine Geradenspiegelung an einer Geraden d mit 
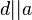und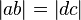 
.
Beweis:
Satz X.2:
- Die Verkettung von drei Geradenspiegelungen 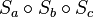, an drei Geraden a, b und c die sich in einem Punkt S schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse d, die durch den Punkt S verläuft mit
.
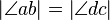Beweis:
Definition X.1 (Schub- oder Gleitspiegelung)
Eine Schub- oder Gleitspiegelung ist eine Abbildung, die bei der Verkettung dreier Geradenspiegelungen 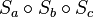entsteht, wenn die zwei Geraden a und b parallel zueinander und die dritte Gerade c senkrecht dazu steht.
Experimentieren Sie mit der nachfolgenden GeoGebra-Applikation. Welche Eigenschaften der Schubspiegelung entdecken Sie?
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Satz X.3:
Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.
Beweis:
