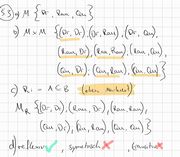Lösung von Aufgabe 5.3 P (WS 20 21): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 10: Zeile 10:
 
  Alles korrekt. Aber ist die Relation wirklich nicht transitiv?
 
  Alles korrekt. Aber ist die Relation wirklich nicht transitiv?
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]
 +
 +
d) ich denke mal, wenn '''Q''' <math>\subseteq </math> '''Rau''' <math> \wedge </math> '''Rau''' <math>\subseteq </math> '''Dr''' <math> \Rightarrow </math> '''Q''' <math>\subseteq </math> '''Dr''' , also ist die Relation auch transitiv.--[[Benutzer:Pi-mal-Daumen|Pi-mal-Daumen]] ([[Benutzer Diskussion:Pi-mal-Daumen|Diskussion]]) 21:10, 15. Feb. 2021 (CET)

Aktuelle Version vom 15. Februar 2021, 21:10 Uhr

a) Geben Sie die Menge M aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge M \times M.
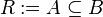c) Wir definineren eine Relation R mit R:=A\subseteq B. Bestimmen Sie die Relation R auf M \times M.
d) Untersuchen Sie die Relation R auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).


Lösung 5.3
Bild "Lösung 5.3" --Hippoo (Diskussion) 18:56, 2. Dez. 2020 (CET) 
Alles korrekt. Aber ist die Relation wirklich nicht transitiv?

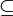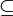d) ich denke mal, wenn Q \subseteq Rau \wedge Rau \subseteq Dr \Rightarrow Q \subseteq 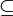Dr , also ist die Relation auch transitiv.--Pi-mal-Daumen (Diskussion) 21:10, 15. Feb. 2021 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.3_P_(WS_20_21)&oldid=37027“