Diskussion:Lösung von Aufgabe 7.1: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
  
 
Ich würde diesen Schritt einfach mit Definition Halbgerade begründen, da steckt es ja mit drin:
 
Ich würde diesen Schritt einfach mit Definition Halbgerade begründen, da steckt es ja mit drin:
 +
 
<u>'''Definition: Halbgerade <math>AB^+</math>'''</u>
 
<u>'''Definition: Halbgerade <math>AB^+</math>'''</u>
 
::Gegeben seien zwei verschiedene Punkte <math>\ A</math> und <math>\ B</math>. Unter dem Strahl bzw. der Halbgeraden <math>\ AB^+</math> versteht man die Strecke <math>\overline{AB}</math> vereinigt mit der Menge aller der Punkte, die man erhält, wenn man <math>\overline{AB}</math> über <math>\ B</math> hinaus verlängert.
 
::Gegeben seien zwei verschiedene Punkte <math>\ A</math> und <math>\ B</math>. Unter dem Strahl bzw. der Halbgeraden <math>\ AB^+</math> versteht man die Strecke <math>\overline{AB}</math> vereinigt mit der Menge aller der Punkte, die man erhält, wenn man <math>\overline{AB}</math> über <math>\ B</math> hinaus verlängert.
 +
--[[Benutzer:Principella|Principella]] 15:16, 26. Jul. 2010 (UTC)

Version vom 26. Juli 2010, 16:16 Uhr

Voraussetzung: Strecke 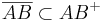\overline{AB}\subset AB^+
Behauptung: es existiert genau eine Strecke \overline{AB^{*}} mit \left| AB^{*} \right| = \pi \left| AB \right| und \overline{AB} \subset \overline{AB^{*}}

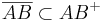So steht es in der Lösung. Aber wie kann ich von dieser Voraussetzung ausgehen? Meines Erachtens ist die Voraussetzung, dass eine Strecke \overline{AB} existiert und damit fertig, oder? --Maude001 09:05, 25. Jul. 2010 (UTC) P.S. Natürlich ist \overline{AB}\subset AB^+ logisch, aber kann man denn von logischen Dingen ausgehen, ohne zu Begründen?

Ich würde diesen Schritt einfach mit Definition Halbgerade begründen, da steckt es ja mit drin:

Definition: Halbgerade AB^+

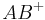Gegeben seien zwei verschiedene Punkte \ A und \ B. Unter dem Strahl bzw. der Halbgeraden \ AB^+ versteht man die Strecke \overline{AB} vereinigt mit der Menge aller der Punkte, die man erhält, wenn man \overline{AB} über \ B hinaus verlängert.

--Principella 15:16, 26. Jul. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Diskussion:Lösung_von_Aufgabe_7.1&oldid=3787“