Lösung von Aufgabe 1.2 (SoSe 22): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.<br /><br /> <math>M_1 = \{x\vert x\in \mathbb{N}\wedg…“) |
Kwd077 (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
<math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br /> | <math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br /> | ||
| − | + | M<sub>1</sub>: x+2=0 → x=-2 → x<s>€</s> N → M<sub>1</sub>=<s>O</s> → M<sub>1</sub>= [] | |
| − | + | M<sub>2</sub>: x<sup>2</sup>+2=0 → x<sup>2</sup>=-2 → x=√-2 → √-2 <s>€</s>R → M<sub>2</sub>=<s>O</s> → M<sub>2</sub>= [] | |
| + | M<sub>3</sub>: x+2=0 → x=-2 → -2€Z → <sub>3</sub>M= [-2] | ||
| + | M<sub>4</sub>: x<sup>2</sup>-2=0 → x<sup>2</sup>=2 → x=√2 → √2<s>€</s>Q → M<sub>4</sub>=<s>O</s> → M=[] | ||
| + | M<sub>5</sub>: x<sup>2</sup>-2=0 → x<sup>2</sup>=2 → x=√2,-√2 → √2,-√€R → M<sub>5</sub>[-√2,√2] | ||
| + | M<sub>6</sub>: (x+2)<sup>2</sup>=0 → x+2=√0 → x=-2 → x€R → M<sub>6</sub>= [-2] | ||
| + | M<sub>1</sub>=M<sub>2</sub>=M<sub>4</sub> | ||
| + | M<sub>3</sub>=M<sub>6</sub>--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 21:21, 10. Apr. 2022 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 10. April 2022, 20:21 Uhr
Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.
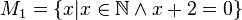
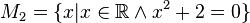
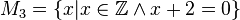
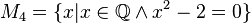
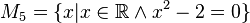
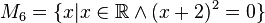
M1: x+2=0 → x=-2 → x€ N → M1=O → M1= []
M2: x2+2=0 → x2=-2 → x=√-2 → √-2 €R → M2=O → M2= []
M3: x+2=0 → x=-2 → -2€Z → 3M= [-2]
M4: x2-2=0 → x2=2 → x=√2 → √2€Q → M4=O → M=[]
M5: x2-2=0 → x2=2 → x=√2,-√2 → √2,-√€R → M5[-√2,√2]
M6: (x+2)2=0 → x+2=√0 → x=-2 → x€R → M6= [-2]
M1=M2=M4
M3=M6--Kwd077 (Diskussion) 21:21, 10. Apr. 2022 (CEST)

