Benutzer:Hsu2002: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „=== Ein Rechteck versteckt in einer Taschentuchbox. === 300px Der Flächeninhalt A der grün umrandeten Fläche lä…“) |
(→Ein Rechteck versteckt in einer Taschentuchbox.) |
||
| Zeile 3: | Zeile 3: | ||
Der Flächeninhalt A der grün umrandeten Fläche lässt sich durch folgende Formel berechnen: <math>A=a*b</math> . | Der Flächeninhalt A der grün umrandeten Fläche lässt sich durch folgende Formel berechnen: <math>A=a*b</math> . | ||
| + | |||
Wenn man die rechteckige Box in eine runde Schachtel stellen möchte, da diese schöner aussieht, so muss die runde Schachtel mindestens einen Radius der Formel <math>(\sqrt{ a^{2} + b^{2} }) \div 2</math> besitzen. | Wenn man die rechteckige Box in eine runde Schachtel stellen möchte, da diese schöner aussieht, so muss die runde Schachtel mindestens einen Radius der Formel <math>(\sqrt{ a^{2} + b^{2} }) \div 2</math> besitzen. | ||
| + | |||
Das Volumen der Box lässt sich über die Formel <math>V=a*b*c</math> berechnen. | Das Volumen der Box lässt sich über die Formel <math>V=a*b*c</math> berechnen. | ||
Aktuelle Version vom 11. April 2022, 20:44 Uhr
Ein Rechteck versteckt in einer Taschentuchbox.
Der Flächeninhalt A der grün umrandeten Fläche lässt sich durch folgende Formel berechnen: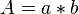 
.
Wenn man die rechteckige Box in eine runde Schachtel stellen möchte, da diese schöner aussieht, so muss die runde Schachtel mindestens einen Radius der Formel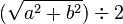 
besitzen.
Das Volumen der Box lässt sich über die Formel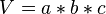 
berechnen.
