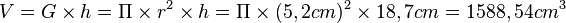Benutzerin:Roecklh: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „MannheimPuzzle Dose Auf dem Bild ist eine zylinderförmige Puzzledose zusehen. Sie hat folgende Maße: d= 10,4 cm r=…“) |
|||
| Zeile 10: | Zeile 10: | ||
Damit lassen sich folgende Rechnungen berechnen: | Damit lassen sich folgende Rechnungen berechnen: | ||
| − | <math> G= \Pi \times r^{2} = \Pi \times (5,2cm)^{2} = 84,95cm^{2} </math> | + | Grundfläche: <math> G= \Pi \times r^{2} = \Pi \times (5,2cm)^{2} = 84,95cm^{2} </math> |
| − | <math> U= 2 \times \Pi \times r= 2 \times \Pi \times 5,2cm= 32,67cm </math> | + | Umfang: <math> U= 2 \times \Pi \times r= 2 \times \Pi \times 5,2cm= 32,67cm </math> |
| − | <math> M=U \times h=2 \times \Pi \times r \times h=2 \times \Pi \times 5,2cm \times 18,7cm= 610,98 cm^{2} </math> | + | Mantelfläche: <math> M=U \times h=2 \times \Pi \times r \times h=2 \times \Pi \times 5,2cm \times 18,7cm= 610,98 cm^{2} </math> |
| − | <math> O=2 \times G + M=2( \Pi \times r^{2} ) + 2 \times \Pi \times r \times h=2( \Pi \times (5,2cm)^{2} ) + 2 \times \Pi \times 5,2cm \times 18,7cm=780,87cm^{2} | + | Oberfläche: <math> O=2 \times G + M=2( \Pi \times r^{2} ) + 2 \times \Pi \times r \times h=2( \Pi \times (5,2cm)^{2} ) + 2 \times \Pi \times 5,2cm \times 18,7cm=780,87cm^{2} |
</math> | </math> | ||
| − | <math> V=G \times h= \Pi \times r^{2} \times h= \Pi \times (5,2cm)^{2} \times 18,7cm=1588,54cm^{3} </math> | + | Volumen: <math> V=G \times h= \Pi \times r^{2} \times h= \Pi \times (5,2cm)^{2} \times 18,7cm=1588,54cm^{3} </math> |
Aktuelle Version vom 15. April 2022, 15:44 Uhr
Auf dem Bild ist eine zylinderförmige Puzzledose zusehen. Sie hat folgende Maße:
d= 10,4 cm
r= 5,2 cm
h= 18,7 cm
Damit lassen sich folgende Rechnungen berechnen:
Grundfläche: 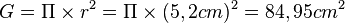
Umfang: 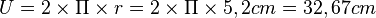
Mantelfläche: 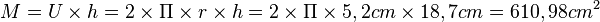
Oberfläche: 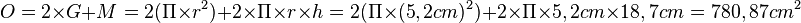
Volumen: