Lösung von Aufgabe 9.5P (SoSe 22): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\…“) |
Kwd077 (Diskussion | Beiträge) |
||
| Zeile 5: | Zeile 5: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| + | Kontraposition: P ist kein Element von m, daraus folgt Abstand AP ist nicht gleich dem Abstand PB | ||
| + | |||
| + | Vor: Abstand AP ist gleich dem Abstand PB, m ist Mittelsenkrechte von der Strecke AB | ||
| + | Beh: P ist Element von m | ||
| + | Annahme: P ist kein Element von m | ||
| + | |||
| + | Beweis: | ||
| + | 1. Strecke BP schneidet m ergibt leere Menge, Begründung : Annahme | ||
| + | 2. Strecke AP schneidet m ergibt den Punkt R, Begründung: 1., (Skizze auf welcher ich den Punkt P in die Halbebene von Punkt B gezeichnet habe) | ||
| + | 3. Abstand AR ist gleich dem Abstand RB, Begründung: 2., Mittelsenkrechtenkriterium | ||
| + | 4. Abstand AB + Abstand BP > Abstand AP, Begründung: 3., Dreiecksungleichung(die Summe der Strecke AB + BC ist immer > AC) | ||
| + | 5. Abstand AR + Abstand BR > Abstand AB, Begründung: Dreiecksungleichung | ||
| + | 6. m schneidet Strecke AP und Strecke Strecke AB, Begründung: 2., Satz von Pasch | ||
| + | 7. Abstand AR + Abstand RP = Abstand AP, Begründung 2., Zwischenrelation | ||
| + | 8. Abstand AP ist ungleich dem Abstand AB , Begründung: 4., 5., 7. | ||
| + | 9. Widerspruch zur Voraussetzung, Annahme ist zu verwerfen--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 12:01, 22. Jun. 2022 (CEST) | ||
Version vom 22. Juni 2022, 11:01 Uhr
m sei Mittelsenkrechte der Strecke  . Beweisen Sie durch Kontraposition:
. Beweisen Sie durch Kontraposition: 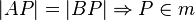
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Kontraposition: P ist kein Element von m, daraus folgt Abstand AP ist nicht gleich dem Abstand PB
Vor: Abstand AP ist gleich dem Abstand PB, m ist Mittelsenkrechte von der Strecke AB Beh: P ist Element von m Annahme: P ist kein Element von m
Beweis: 1. Strecke BP schneidet m ergibt leere Menge, Begründung : Annahme 2. Strecke AP schneidet m ergibt den Punkt R, Begründung: 1., (Skizze auf welcher ich den Punkt P in die Halbebene von Punkt B gezeichnet habe) 3. Abstand AR ist gleich dem Abstand RB, Begründung: 2., Mittelsenkrechtenkriterium 4. Abstand AB + Abstand BP > Abstand AP, Begründung: 3., Dreiecksungleichung(die Summe der Strecke AB + BC ist immer > AC) 5. Abstand AR + Abstand BR > Abstand AB, Begründung: Dreiecksungleichung 6. m schneidet Strecke AP und Strecke Strecke AB, Begründung: 2., Satz von Pasch 7. Abstand AR + Abstand RP = Abstand AP, Begründung 2., Zwischenrelation 8. Abstand AP ist ungleich dem Abstand AB , Begründung: 4., 5., 7. 9. Widerspruch zur Voraussetzung, Annahme ist zu verwerfen--Kwd077 (Diskussion) 12:01, 22. Jun. 2022 (CEST)

