Lösung von Zusatzaufgabe 1 (WS 23 24): Unterschied zwischen den Versionen
End007 (Diskussion | Beiträge) |
(→Aufgabe 1) |
||
| Zeile 11: | Zeile 11: | ||
So habe es versucht zu verbessern [[Datei:Zusatzaufgabe verbessert.jpeg|thumb|Zusatz verbessert]]--[[Benutzer:Capricorn|Capricorn]] ([[Benutzer Diskussion:Capricorn|Diskussion]]) 21:34, 25. Okt. 2023 (CEST) | So habe es versucht zu verbessern [[Datei:Zusatzaufgabe verbessert.jpeg|thumb|Zusatz verbessert]]--[[Benutzer:Capricorn|Capricorn]] ([[Benutzer Diskussion:Capricorn|Diskussion]]) 21:34, 25. Okt. 2023 (CEST) | ||
| + | |||
| + | Deine Verbesserung zeigt nun noch mehr richtige Teilmengenbeziehungen :) Gibt es Parallelogramme, die keine allgemeinen Trapeze sind?--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 20:03, 27. Okt. 2023 (CEST) | ||
| Zeile 19: | Zeile 21: | ||
[[Datei:Teilmengenbeziehungen Vierecke.jpeg|thumb|Das wäre mein Vorschlag.]]--[[Benutzer:End007|End007]] ([[Benutzer Diskussion:End007|Diskussion]]) 18:43, 26. Okt. 2023 (CEST) | [[Datei:Teilmengenbeziehungen Vierecke.jpeg|thumb|Das wäre mein Vorschlag.]]--[[Benutzer:End007|End007]] ([[Benutzer Diskussion:End007|Diskussion]]) 18:43, 26. Okt. 2023 (CEST) | ||
| + | |||
| + | Hi End007 bei deinem Entwurf sind die Mengen schon in der richtigen Größe eingezeichnet. Leider zeigt er die Teilmengenbeziehungen noch nicht richtig. Ich mache einmal ein Beispiel um dir zu zeigen, worüber du nochmal nachdenken "musst": Ein Quadrat vereint die Eigenschaften von Raute und Rechteck. Somit ist jedes Quadrat ein Rechteck und gleichzeitig auch eine Raute. Es gibt aber Rauten, die keine Rechtecke sind und umgekehrt. Bei deinem Venndiagramm sieht es so aus, als ob die meisten Quadrate Rechtecke wären und einige Quadrate Rauten wären, es allerdings keine Rauten gibt, die gleichzeitig auch Rechtecke sind. (Dabei sind ja alle Quadrate gleichzeitig Rechtecke und Rauten) | ||
| + | Ich hoffe das hilft dir weiter :)--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 20:03, 27. Okt. 2023 (CEST) | ||
Version vom 27. Oktober 2023, 19:03 Uhr
Aufgabe 1
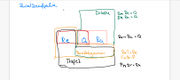
Erstellen Sie zu den Vierecksarten aus Aufgabe 2.2 ein Venndiagramm, aus dem die Teilmengenbeziehungen der Mengen sichtbar werden. (Ausgenommen Schiefer Drache; gleichschenkliges Trapez)--Capricorn (Diskussion) 10:35, 25. Okt. 2023 (CEST)Hi Capricorn super, dass du dich an diese schwierige Zusatzaufgabe getraut hast. Du stellst schon viele Teilmengenbeziehungen richtig dar. :) Überlege dir noch einmal ob in deinem Venn Diagramm wirklich alle Teilmengenbeziehungen von Quadrat und Raute dargestellt sind. Gibt es Drachen, die weder Raute noch Quadrat, aber dennoch Parallelogramme sind?--Matze2000 (Diskussion) 15:12, 25. Okt. 2023 (CEST)
So habe es versucht zu verbessern --Capricorn (Diskussion) 21:34, 25. Okt. 2023 (CEST)Deine Verbesserung zeigt nun noch mehr richtige Teilmengenbeziehungen :) Gibt es Parallelogramme, die keine allgemeinen Trapeze sind?--Matze2000 (Diskussion) 20:03, 27. Okt. 2023 (CEST)
Hi End007 bei deinem Entwurf sind die Mengen schon in der richtigen Größe eingezeichnet. Leider zeigt er die Teilmengenbeziehungen noch nicht richtig. Ich mache einmal ein Beispiel um dir zu zeigen, worüber du nochmal nachdenken "musst": Ein Quadrat vereint die Eigenschaften von Raute und Rechteck. Somit ist jedes Quadrat ein Rechteck und gleichzeitig auch eine Raute. Es gibt aber Rauten, die keine Rechtecke sind und umgekehrt. Bei deinem Venndiagramm sieht es so aus, als ob die meisten Quadrate Rechtecke wären und einige Quadrate Rauten wären, es allerdings keine Rauten gibt, die gleichzeitig auch Rechtecke sind. (Dabei sind ja alle Quadrate gleichzeitig Rechtecke und Rauten) Ich hoffe das hilft dir weiter :)--Matze2000 (Diskussion) 20:03, 27. Okt. 2023 (CEST)