Lösung von Aufgabe 10.2P (WS 23 24): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.2:<br /> Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S'', sowie zwei Punkten <math>A\in a</math…“) |
|||
| Zeile 6: | Zeile 6: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
| + | |||
| + | |||
| + | [[Datei:Vorschlag Capricorn 10.2.jpeg|thumb|Vorschlag Capricorn 10.2]]--[[Benutzer:Capricorn|Capricorn]] ([[Benutzer Diskussion:Capricorn|Diskussion]]) 21:32, 9. Jan. 2024 (CET) | ||
Version vom 9. Januar 2024, 21:32 Uhr
Beweisen Sie Satz IX.2:
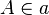 und
und 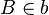 , die von S jeweils verschieden sind. Wir betrachten die Verkettung
, die von S jeweils verschieden sind. Wir betrachten die Verkettung  . Für einen beliebigen Punkt P und seinen Bildpunkt
. Für einen beliebigen Punkt P und seinen Bildpunkt  gilt:
gilt: 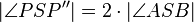 .
.--Capricorn (Diskussion) 21:32, 9. Jan. 2024 (CET)


