Satz des Pythagoras WS 23 24: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
a) Bewege den Punkt '''C''', der auf dem Kreis entlangläuft. Halte dafür die linke Maustaste gedrückt und bewege die Maus entlang des Kreises. | a) Bewege den Punkt '''C''', der auf dem Kreis entlangläuft. Halte dafür die linke Maustaste gedrückt und bewege die Maus entlang des Kreises. | ||
| + | |||
| + | <ggb_applet id="jy6msgsr" width="1320" height="798" border="888888" /> | ||
b) Was kannst du '''beobachten'''? | b) Was kannst du '''beobachten'''? | ||
| Zeile 12: | Zeile 14: | ||
Besprich deine Beobachtungen mit deinem Sitznachbarn/deiner Sitznachbarin. | Besprich deine Beobachtungen mit deinem Sitznachbarn/deiner Sitznachbarin. | ||
| − | d) Was ihr besprochen habt, hat schon der antike griechische Mathematiker '''Thales von Milet''' ca. 500 v.Chr. beobachtet! Er hat seine Beobachtungen in einem Satz festgehalten, welchen man den "Satz des Thales" nennt. Vervollständigt nun den '''Satz des Thales''' mit euren Beobachtungen: | + | d) Was ihr besprochen habt, hat schon der antike griechische Mathematiker '''Thales von Milet''' ca. 500 v.Chr. beobachtet! Er hat seine Beobachtungen in einem Satz festgehalten, welchen man den "Satz des Thales" nennt. Vervollständigt nun den '''Satz des Thales''' mit euren Beobachtungen und schreibt ihn in euer Heft: |
Liegt der Punkt C eines _____________ auf einem Halbkreis über der Strecke ___________, dann hat das Dreieck am Punkt _______ immer einen ___________ | Liegt der Punkt C eines _____________ auf einem Halbkreis über der Strecke ___________, dann hat das Dreieck am Punkt _______ immer einen ___________ | ||
Version vom 14. Februar 2024, 13:34 Uhr
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Inhaltsverzeichnis |
Aufgabe 1: Wiederholung Satz des Thales
a) Bewege den Punkt C, der auf dem Kreis entlangläuft. Halte dafür die linke Maustaste gedrückt und bewege die Maus entlang des Kreises.
b) Was kannst du beobachten?
Besprich deine Beobachtungen mit deinem Sitznachbarn/deiner Sitznachbarin.
c) Beobachte nun den Winkel α: Verändert sich seine Größe, wenn du den Punkt C bewegst?
Besprich deine Beobachtungen mit deinem Sitznachbarn/deiner Sitznachbarin.
d) Was ihr besprochen habt, hat schon der antike griechische Mathematiker Thales von Milet ca. 500 v.Chr. beobachtet! Er hat seine Beobachtungen in einem Satz festgehalten, welchen man den "Satz des Thales" nennt. Vervollständigt nun den Satz des Thales mit euren Beobachtungen und schreibt ihn in euer Heft:
Liegt der Punkt C eines _____________ auf einem Halbkreis über der Strecke ___________, dann hat das Dreieck am Punkt _______ immer einen ___________ ___________.
Erinnerung: Rechtwinklige Dreiecke
Ein rechtwinkliges Dreieck hat immer zwei Katheten und eine Hypothenuse. Die Hypothenuse ist die längste Seite und liegt immer gegenüber vom rechten Winkel. Die anderen beiden Seiten sind die Katheten.
Aufgabe 2: Hinführung zum Satz des Pythagoras
Das Dreieck, das du eben schon in der Aufgabe zum Satz des Thales untersucht hast, wurde nun mit den drei Flächen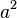 
, 
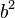und 
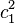ergänzt. Die Flächen wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a = 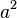= blaue Fläche). Die Flächen sind deshalb quadratisch.
a) Bewege nun erneut den Punkt C und beobachte, wie sich die Flächen 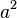, 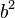und 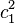verändern.
Besprich dich mit deinem Sitznachbarn/deiner Sitznachbarin.
Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Aussagen mit „wahr“ oder „falsch“ bewertet.
| Aussage | wahr | falsch |
|---|---|---|
| Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche . |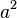
||
| Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche . |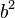
||
| Wenn man den Punkt C bewegt, dann verändert sich die Größe der Fläche . |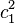
Aufgabe 3: Der Satz des Pythagoras
Gut beobachtet! Die Größe der Fläche 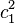verändert sich nicht. Du fragst dich bestimmt, woran das liegt. Eine Erklärung liefert dir der Satz des Pythagoras!
Der Satz des Pythagoras: In einem rechtwinkligen Dreieck ist die Summe der Quadrate der Katheten genauso groß wie das Quadrat der Hypotenuse.
Daher gilt: + =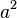 
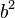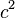
Die Summe der Flächen der Katheten (in unserem Dreieck also 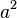+ 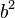) ist also immer genauso groß, wie die Fläche der Hypothenuse (in unserem Beispiel 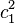). Ganz egal, ob 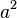kleiner als 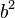ist, oder andersherum.
