Lösung von Aufg. 7.3: Unterschied zwischen den Versionen

Version vom 23. November 2010, 16:02 Uhr

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.

1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

Es seien und 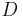drei Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei der Punkte vier Punkte , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...