Lösung von Aufg. 10.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 4: | Zeile 4: | ||
| − | 1)<math>| \angle ASW| </math> = <math| \angle WSB | | + | 1)<math>| \angle ASW| </math> = <math>| \angle WSB| </math>__________________Def. Winkelhalbierende<br /> |
| − | 2)<math| \angle ASW | | + | 2)<math>| \angle ASW| </math>+<math>| \angle WSB| </math> = <math>| \angle ASB| </math>____________Winkeladditionsaxiom<br /> |
| − | 3)<math| \angle ASW | | + | 3)<math>| \angle ASW| </math> +<math>| \angle ASW| </math>= <math>| \angle ASB| </math>________________1) und 2)<br /> |
| − | 4)2 <math| \angle ASW | | + | 4)2 <math>| \angle ASW| </math>= )<math| \angle ASB |></math>____________________3)<br /> |
| − | 5)<math| \angle ASW |></math>= <math> | + | 5)<math| \angle ASW |></math>= <math>| \angle ASB| </math>_________________Rechnen in R<br /> |
6)<math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.________________________1) und 5)--[[Benutzer:Engel82|Engel82]] 16:35, 15. Dez. 2010 (UTC) | 6)<math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.________________________1) und 5)--[[Benutzer:Engel82|Engel82]] 16:35, 15. Dez. 2010 (UTC) | ||
Version vom 15. Dezember 2010, 17:41 Uhr
Beweisen Sie Satz VI.eineinhalb
Es seidie Winkelhalbierende des Winkels
. Dann gilt
.
1)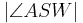 =
= 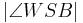 __________________Def. Winkelhalbierende
__________________Def. Winkelhalbierende
2)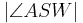 +
+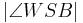 =
= 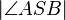 ____________Winkeladditionsaxiom
____________Winkeladditionsaxiom
3)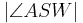 +
+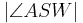 =
= 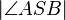 ________________1) und 2)
________________1) und 2)
4)2 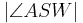 = )<math| \angle ASB |></math>____________________3)
= )<math| \angle ASB |></math>____________________3)
5)<math| \angle ASW |></math>= 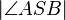 _________________Rechnen in R
_________________Rechnen in R
6)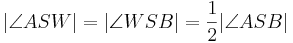 .________________________1) und 5)--Engel82 16:35, 15. Dez. 2010 (UTC)
.________________________1) und 5)--Engel82 16:35, 15. Dez. 2010 (UTC)

