Lösung von Aufg. 11.4: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Beweisen Sie Satz VII.6 b ::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A<...)
 
Zeile 4: Zeile 4:
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]
 +
 +
 +
<p>--------------------------------------------------------------------</p>
 +
 +
'''Voraussetzung:'''Es sei eine Strecke <math> \overline{AB} </math> und ein Punkt <math> P \in m </math> , m ist Mittelsenkrechte von <math>\overline{AB}</math>
 +
<br />
 +
 +
<br />'''Behauptung:''' <math>\overline{PA} \cong \overline{PB}</math>
 +
 +
 +
 +
{| class="wikitable "
 +
|+ Beweis
 +
! style="background: #A2CD5A;" |Nr.
 +
! style="background: #A2CD5A;" |Beweisschritt
 +
! style="background: #A2CD5A;" |Begründung
 +
|-
 +
! style="background: #EEE685;"|(I)
 +
| <math>m \cap \overline{AB} = \lbrace M \rbrace  </math>, <math>\overline{AM} \cong \overline{BM}</math>
 +
| Def.VI.1 (Mittelsenkrechte)
 +
|-
 +
! style="background: #EEE685;"|(II)
 +
| <math>\overline{PM} \subset m</math>
 +
| I, Vor.(<math>P \in m</math>)
 +
|-
 +
! style="background: #EEE685;"|(III)
 +
| <math>\angle PMA \cong \angle PMB</math>
 +
| II, Def.VI.1 (Mittelsenkrechte)
 +
|-
 +
! style="background: #EEE685;"|(IV)
 +
| <math>\overline{PM} \cong \overline{PM}</math>
 +
| Reflexivität der Kongruenz
 +
|-
 +
! style="background: #EEE685;"|(V)
 +
| <math>\triangle AMP \cong \triangle MBP</math>
 +
| I, III, IV, Axiom V (SWS)
 +
|-
 +
! style="background: #EEE685;"|(VI)
 +
| <math>\overline{PA} \cong \overline{PB}</math>
 +
| V, Def. VII.3 (Dreieckskongruenz)
 +
|-
 +
 +
|}
 +
 +
'''qed.'''<br />
 +
 +
--[[Benutzer:Studentxyz|Studentxyz]] 23:02, 17. Jan. 2011 (UTC)
 +
<p>--------------------------------------------------------------------</p>

Version vom 18. Januar 2011, 01:02 Uhr

Beweisen Sie Satz VII.6 b

Wenn ein Punkt \ P zur Mittelsenkrechten der Strecke \overline{AB} gehört, dann hat er zu den Punkten \ A und \ B ein und denselben Abstand.


--------------------------------------------------------------------

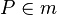Voraussetzung:Es sei eine Strecke \overline{AB} und ein Punkt P \in m , m ist Mittelsenkrechte von \overline{AB}


Behauptung: 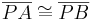\overline{PA} \cong \overline{PB}


Beweis
Nr. Beweisschritt Begründung
(I) 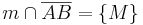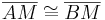m \cap \overline{AB} = \lbrace M \rbrace , \overline{AM} \cong \overline{BM} Def.VI.1 (Mittelsenkrechte)
(II) 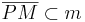\overline{PM} \subset m I, Vor.(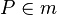P \in m)
(III) 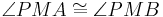\angle PMA \cong \angle PMB II, Def.VI.1 (Mittelsenkrechte)
(IV) 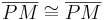\overline{PM} \cong \overline{PM} Reflexivität der Kongruenz
(V) 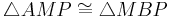\triangle AMP \cong \triangle MBP I, III, IV, Axiom V (SWS)
(VI) 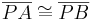\overline{PA} \cong \overline{PB} V, Def. VII.3 (Dreieckskongruenz)

qed.

--Studentxyz 23:02, 17. Jan. 2011 (UTC)

--------------------------------------------------------------------

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._11.4&oldid=5972“