Lösung von Aufg. 12.6: Unterschied zwischen den Versionen
(→Aufgabe 12.6) |
(→Aufgabe 12.6) |
||
| Zeile 20: | Zeile 20: | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| + | |||
| + | Andere Möglichkeit, könnte das gehen? | ||
| + | |||
| + | Vor.: aIIb | ||
| + | |||
| + | Beh.: IαI = IβI | ||
| + | |||
| + | 1) aIIb_____________________________Vor. | ||
| + | |||
| + | 2) IαI+IάI=180_______________________1), Supplementaxiom, Definition Nebenwinkel | ||
| + | |||
| + | 3) IάI=Iβ’I___________________________Stufenwinkelsatz | ||
| + | |||
| + | 4) IβI+Iβ’I=180_______________________1), Supplementaxiom, Definition Nebenwinkel | ||
| + | |||
| + | 5) IαI+I β’I=180______________________2),3),4) | ||
| + | |||
| + | 6) IαI=IβI___________________________5) | ||
| + | |||
| + | 7) Behauptung stimmt | ||
Version vom 25. Januar 2011, 17:47 Uhr
Aufgabe 12.6
Beweisen Sie den Stufenwinkelsatz.
Vor: a//b
Beh: 


Annahme:  ist nicht kongruent zu
ist nicht kongruent zu 
1) Es existiert genau eine Gerade h für die gilt:___________________________WInkelkonstruktionsaxiom
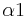


2) h//b________________________Umkehrung des Stufenwinkelsatzes und 1)
3) Die Gerade b hat zwei Parallelen a und h______________________ Vor. und 2) Widerspruch zum EPA
4) a=h___________________________2)
5) Annahme ist zu verwerfen
6) Behauptung stimmt --Engel82 17:57, 19. Jan. 2011 (UTC)
Musst du für diesen Beweis nicht erstmal die Umkehrung des Stufenwinkelsatz beweisen...das haben wir ja noch nicht gemacht?!
Andere Möglichkeit, könnte das gehen?
Vor.: aIIb
Beh.: IαI = IβI
1) aIIb_____________________________Vor.
2) IαI+IάI=180_______________________1), Supplementaxiom, Definition Nebenwinkel
3) IάI=Iβ’I___________________________Stufenwinkelsatz
4) IβI+Iβ’I=180_______________________1), Supplementaxiom, Definition Nebenwinkel
5) IαI+I β’I=180______________________2),3),4)
6) IαI=IβI___________________________5)
7) Behauptung stimmt

