Übung Aufgaben 1 (SoSe 11): Unterschied zwischen den Versionen
(→Aufgabe 1.1) |
(→Aufgabe 1.1) |
||
| Zeile 27: | Zeile 27: | ||
[[Lösung von Aufgabe 1.1 (SoSe_11)]] | [[Lösung von Aufgabe 1.1 (SoSe_11)]] | ||
| − | 1 ist eine Definition ( n-Eck ist der Oberbegriff-muss bekannt sein, Merkmal n= 4) | + | 1 ist eine Definition ( n-Eck ist der Oberbegriff-muss bekannt sein, Merkmal n= 4); |
| − | 2. Definition ( Fakultät) | + | 2. Definition ( Fakultät); |
| − | 3. keine Definition, kann man beweisen | + | 3. keine Definition, kann man beweisen; |
| − | 4. Definition | + | 4. Definition; |
| − | 5. Definition ( gibt es Dreicksschneidende? ) | + | 5. Definition ( gibt es Dreicksschneidende? ) ; |
| − | 6. keine Definition - Aussage ? | + | 6. keine Definition - Aussage ?; |
7. falsch - auch ein 5- Eck hat vier Ecken--[[Benutzer:Mathefix|Mathefix]] 11:59, 12. Apr. 2011 (CEST) | 7. falsch - auch ein 5- Eck hat vier Ecken--[[Benutzer:Mathefix|Mathefix]] 11:59, 12. Apr. 2011 (CEST) | ||
Version vom 12. April 2011, 11:00 Uhr
Inhaltsverzeichnis |
Aufgaben zu Definitionen
Aufgabe 1.1
In welchen Fällen handelt es sich um Definitionen? Begründen Sie!
- Jedes n-Eck mit n=4 heißt Viereck.
-
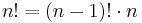 , falls
, falls 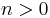
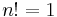 , falls
, falls 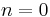
- Stufenwinkel an geschnittenen Parallelen sind kongruent.
- Jedes Dreieck mit einem Umkreis heißt Sehnendreieck.
- Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
- Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
- Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
- Jedes Viereck mit einem Umkreis heißt Sehnenviereck.
- Es gibt Sehnenvierecke.
- Punkt vor Strich.
- Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
- Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
- Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
- Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
- Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
- Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
- Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
- Ein Rechteck hat vier rechte Innenwinkel.
- Ein Quadrat ist ein Rechteck.
- Jedes Quadrat ist ein Rechteck.
- Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.
Lösung von Aufgabe 1.1 (SoSe_11)
1 ist eine Definition ( n-Eck ist der Oberbegriff-muss bekannt sein, Merkmal n= 4); 2. Definition ( Fakultät); 3. keine Definition, kann man beweisen; 4. Definition; 5. Definition ( gibt es Dreicksschneidende? ) ; 6. keine Definition - Aussage ?; 7. falsch - auch ein 5- Eck hat vier Ecken--Mathefix 11:59, 12. Apr. 2011 (CEST)
Aufgabe 1.2
Definieren Sie die folgenden Begriffe mathematisch korrekt:
Viereck, Trapez, Parallelogramm, Drachen, Raute, Rechteck, Quadrat
Lösung von Aufgabe 1.2 (SoSe_11)
Ein Viereck ist eine geometrische Figur mit genau 4 Ecken.--Mathefix 11:55, 12. Apr. 2011 (CEST)
Aufgabe 1.3
Definitionen_in_der_Mathematik_SoSe_11#.C3.9Cbungsaufgabe_1.3_der_ersten_Serie
Aufgabe 1.4
Am 03. Febr. 2003 wurde in der Quiz-Sendung "Wer wird Millionär" folgende 16000 €-Frage gestellt:
Jedes Rechteck ist ein ...
Mit folgenden Auswahlantworten: Rhombus (Raute), Quadrat, Trapez, Parallelogramm
Nehmen Sie Stellung!
Lösung von Aufgabe 1.3 (SoSe_11)
Aufgabe 1.5
Definitionen_in_der_Mathematik_SoSe_11#.C3.9Cbungsaufgabe_1.5_der_Serie_1

