Diskussion:Lösung von Aufgabe 3.3 (SoSe11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „==Hinweis zur Lösung der Aufgabe== --~~~~ Es sei <math>\ w_1</math> die Winkelhalbierende des Winkels <math>\angle{ASB}</math> entsprechend der Definition:<br />…“) |
*m.g.* (Diskussion | Beiträge) (→Hinweis zur Lösung der Aufgabe) |
||
| Zeile 3: | Zeile 3: | ||
Es sei <math>\ w_1</math> die Winkelhalbierende des Winkels <math>\angle{ASB}</math> entsprechend der Definition:<br /> | Es sei <math>\ w_1</math> die Winkelhalbierende des Winkels <math>\angle{ASB}</math> entsprechend der Definition:<br /> | ||
# <math>\ w_1</math> ist ein Strahl mit dem Anfangspunkt <math>\ S</math> aus dem Inneren von <math>\angle{ASB}</math>. | # <math>\ w_1</math> ist ein Strahl mit dem Anfangspunkt <math>\ S</math> aus dem Inneren von <math>\angle{ASB}</math>. | ||
| − | # Die beiden Winel, die den Strahl <math>\ w_1</math als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl <math>\ SA^+</math> bzw. <math>\ SB^+</math> sind, sind kongruent (gleich groß) zueinder. | + | # Die beiden Winel, die den Strahl <math>\ w_1</math> als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl <math>\ SA^+</math> bzw. <math>\ SB^+</math> sind, sind kongruent (gleich groß) zueinder. |
Im weiteren gehen wir wieder von dem Winkel <math>\angle{ASB}</math> aus und konstruieren den Strahl <math>\ w_2</math> entsprechend der Konstruktionsvorschrift. | Im weiteren gehen wir wieder von dem Winkel <math>\angle{ASB}</math> aus und konstruieren den Strahl <math>\ w_2</math> entsprechend der Konstruktionsvorschrift. | ||
| Zeile 12: | Zeile 12: | ||
zu zeigen: | zu zeigen: | ||
# <math>\ w_2</math> ist ein Strahl mit dem Anfangspunkt <math>\ S</math> aus dem Inneren von <math>\angle{ASB}</math>. | # <math>\ w_2</math> ist ein Strahl mit dem Anfangspunkt <math>\ S</math> aus dem Inneren von <math>\angle{ASB}</math>. | ||
| − | # Die beiden Winel, die den Strahl <math>\ w_2</math als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl <math>\ SA^+</math> bzw. <math>\ SB^+</math> sind, sind kongruent (gleich groß) zueinder. | + | # Die beiden Winel, die den Strahl <math>\ w_2</math> als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl <math>\ SA^+</math> bzw. <math>\ SB^+</math> sind, sind kongruent (gleich groß) zueinder. |
1. ist entsprechend der Konstruktionsvorschrift trivial. | 1. ist entsprechend der Konstruktionsvorschrift trivial. | ||
<br /> | <br /> | ||
Für den Nachweis von 2. helfen die grundlgende Sätze aus der Schulgeometrie. | Für den Nachweis von 2. helfen die grundlgende Sätze aus der Schulgeometrie. | ||
Version vom 27. April 2011, 22:50 Uhr
Hinweis zur Lösung der Aufgabe
--*m.g.* 23:50, 27. Apr. 2011 (CEST)
Es sei 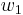 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels 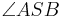 entsprechend der Definition:
entsprechend der Definition:
-
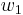 ist ein Strahl mit dem Anfangspunkt
ist ein Strahl mit dem Anfangspunkt  aus dem Inneren von
aus dem Inneren von 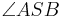 .
.
- Die beiden Winel, die den Strahl
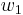 als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl
als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl 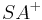 bzw.
bzw. 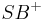 sind, sind kongruent (gleich groß) zueinder.
sind, sind kongruent (gleich groß) zueinder.
Im weiteren gehen wir wieder von dem Winkel 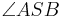 aus und konstruieren den Strahl
aus und konstruieren den Strahl 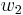 entsprechend der Konstruktionsvorschrift.
entsprechend der Konstruktionsvorschrift.
Behauptung: 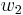 ist auch Winkelhalbierende von
ist auch Winkelhalbierende von 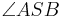 entsprechend der ersten Definition.
entsprechend der ersten Definition.
Beweis:
zu zeigen:
-
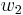 ist ein Strahl mit dem Anfangspunkt
ist ein Strahl mit dem Anfangspunkt  aus dem Inneren von
aus dem Inneren von 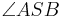 .
.
- Die beiden Winel, die den Strahl
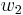 als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl
als gemeinsamen Schenkel haben und deren jeweils anderer Schenkel der Strahl 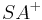 bzw.
bzw. 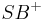 sind, sind kongruent (gleich groß) zueinder.
sind, sind kongruent (gleich groß) zueinder.
1. ist entsprechend der Konstruktionsvorschrift trivial.
Für den Nachweis von 2. helfen die grundlgende Sätze aus der Schulgeometrie.

