Lösung von Aufg. 7.6 (SoSe 11): Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| − | Ich hab mal eine Frage: Was genau heißt die Abkürzung o.B.d.A.? | + | |
| + | |||
| + | Ich hab mal eine Frage: Was genau heißt die Abkürzung o.B.d.A.? --Bayer04 00:09, 25. Mai 2011 (CEST) | ||
Version vom 24. Mai 2011, 23:21 Uhr
Satz:
- Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
- Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
- Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
- Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
Beweis
- Es seien
und 
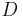vier Punkte, die nicht komplanar sind.
- Es seien
zu zeigen
- ...
Annahme:
- Es gibt drei Punkte von den vier Punkten
, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
- Es gibt drei Punkte von den vier Punkten
ohne komplanar etc: Wenn vier Punkte nicht einer gemeinsamen Ebene angehören, liegen jeweils drei von ihnen nicht auf einer gemeinsamen Geraden.
ohne wenn-dann: Von vier nicht komplanaren Punkten sind je drei nicht kollinear.
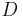Beweis: Es seien und vier Punkte, die nicht komplanar sind.
zu zeigen: je drei dieser Punkte sind nicht kollinear
Annahme: Es gibt drei Punkte von den vier Punkten , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte sein.
Aus Axiom I/4 folgt, dass es für die Punkte 
und den vierten Punkt 
genau eine Ebene gibt - nennen wir sie e, die diese Punkte enthält, da dieses Punktetrio ja eben nicht kollinear ist.
Aus der Annahme folgt, dass auf der gleichen Geraden, nennen wir sie g, liegen, sie sind ja kollinear.
Aus Axiom I/5 folgt, dass die Gerade AB ganz zu der Ebene e gehört, da zwei ihrer Punkte, nämlich zu ihr gehören - schließlich haben wir e ja gerade eben auf den Punkten A, B und D aufgespannt.
Wenn aber die ganze Gerade AB zu e gehört, dann gilt das für jeden Punkt von AB, also auch für C (der ja nach der Annahme kollinear zu A und B ist).
Somit sind A, B, C und D aber doch komplanar, was ein Widerspruch zur Voraussetzung wäre.
(Muss ich den Fall, dass alle vier Punkte kollinear sind, auch noch behandeln? Eigentlich doch nicht, denn bei ihm sind ja auch drei Punkte kollinear und schon das geht nicht, oder? Doch, halt, ich benutze die Konstellation "A,B,D, nicht kollinear" für das Aufspannen der Ebene. Aber wären alle vier kollinear, dürfte ich nach Axiom I/3 einfach einen weiteren, diesmal nicht kollinearen Punkt dazu"erfinden" und dann klappt doch alles, richtig?) --WikiNutzer 22:19, 24. Mai 2011 (CEST)
Ich hab mal eine Frage: Was genau heißt die Abkürzung o.B.d.A.? --Bayer04 00:09, 25. Mai 2011 (CEST)
