Lösung von Aufg. 9.1 (SoSe 11): Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) |
|||
| Zeile 13: | Zeile 13: | ||
Aber sicher bin ich mir auch nicht.--[[Benutzer:Vollyschwamm|Vollyschwamm]] 19:01, 7. Jun. 2011 (CEST) | Aber sicher bin ich mir auch nicht.--[[Benutzer:Vollyschwamm|Vollyschwamm]] 19:01, 7. Jun. 2011 (CEST) | ||
| + | So jetzt nochmal, bevor wieder alles abstürzt :-) | ||
| + | Hier mein Beweisvorschlag, jedoch aus Gründen der schnelleren Schreibweise im Excel erstellt. Problem hierbei ist jedoch, dass Strecken nicht überstrichen werden können. Sie tauchen hier nun (wie in der Schule) in eckigen Klammern auf. | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | [[Bild:Beweis_9_1.JPG]] | ||
| + | |||
| + | |||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 23:50, 7. Jun. 2011 (CEST) | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 7. Juni 2011, 22:50 Uhr
Beweisen Sie: Zu jeder Strecke 
existiert genau eine Strecke 
mit 
und 
.
Kann mir jemand helfen? Ich weiß nicht, was Voraussetzung und was Behauptung ist in diesem Beweis. Kann es sein, dass die Behauptung aus zwei Teilen besteht 1) und 2) ?
Verwendet man hier das Abstandsaxiom und ist dabei der Abstand d =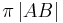 
?
Vielen Dank schonmal :) --Bubble 17:36, 7. Jun. 2011 (CEST)
Ich würde sagen die Vor:
Und du hast recht, es sind zwei Behauptungen. Aber ich habe sie in einem Beweis bewiesen, da man von der ersten Beh auf die zweite Beh kommt.
Aber sicher bin ich mir auch nicht.--Vollyschwamm 19:01, 7. Jun. 2011 (CEST)
So jetzt nochmal, bevor wieder alles abstürzt :-)
Hier mein Beweisvorschlag, jedoch aus Gründen der schnelleren Schreibweise im Excel erstellt. Problem hierbei ist jedoch, dass Strecken nicht überstrichen werden können. Sie tauchen hier nun (wie in der Schule) in eckigen Klammern auf.
--Flo60 23:50, 7. Jun. 2011 (CEST)
