Übung Aufgaben 12 (SoSe 11): Unterschied zwischen den Versionen

Version vom 26. Juni 2011, 17:32 Uhr

Aufgabe 12.1

Definieren Sie den Begriff des gleichschenkligen Dreiecks. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.

Hinweis: Die Schenkel eine Winkels sind Strahlen. Die Schenkel eines gleichschenkligen Dreiecks sind Strecken.

Lösung von Aufg. 12.1 SS11

Aufgabe 12.2

Formulieren Sie den Basiswinkelsatz (Satz VII.5) auf zwei weitere Arten und Weisen.

Lösung von Aufg. 12.2 SS11

Aufgabe 12.3

Beweisen Sie Satz VII.6 a:

Wenn ein Punkt zu den Endpunkten der Strecke jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von .

Lösung von Aufg. 12.3 SS11

Aufgabe 11.4

Beweisen Sie Satz VII.6 b

Wenn ein Punkt zur Mittelsenkrechten der Strecke gehört, dann hat er zu den Punkten und ein und denselben Abstand.

Lösung von Aufg. 11.4

Aufgabe 11.5

Begründen Sie, warum mittels der Sätze Satz VII.6 a und Satz VII.6 b der Satz VII.6 bewiesen wurde.

Lösung von Aufg. 11.5 SS11

Aufgabe 11.6

Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt.

Lösung von Aufg. 11.6 SS11

Aufgabe 11.7

Wenden Sie Ihre Gedankengänge aus Aufgabe 11.5 Analog auf den Begriff des gleichschenkligen Dreiecks an. Inwiefern haben wir es bei dem Basiswinkelsatz und seiner Umkehrung mit einem Kriterium zu tun.

Lösung von Aufg. 11.7 SS11

Aufgabe 11.8

Es seien ein Quadrat und eine positive reelle Zahl, die kleiner als die Seitenlänge von ist. Ferner seien die Punkte 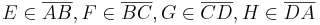mit 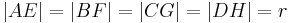gegeben. Man beweise: 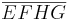ist ein Quadrat.

Lösung von Aufg. 11.8 SS11