Lösung von Aufg. 12.2 SS11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Koooky (Diskussion | Beiträge) |
|||
| Zeile 7: | Zeile 7: | ||
Basiswinkelsatz V2:<br> | Basiswinkelsatz V2:<br> | ||
Sei <math>\overline{ABC}</math> ein Dreieck, wenn <math>\overline{AB} \equiv \overline{BC}</math> dann gilt <math>\angle CAB\equiv \angle BCA</math>.<br>--[[Benutzer:Peterpummel|Peterpummel]] 21:01, 2. Jul. 2011 (CEST) | Sei <math>\overline{ABC}</math> ein Dreieck, wenn <math>\overline{AB} \equiv \overline{BC}</math> dann gilt <math>\angle CAB\equiv \angle BCA</math>.<br>--[[Benutzer:Peterpummel|Peterpummel]] 21:01, 2. Jul. 2011 (CEST) | ||
| + | |||
| + | In jedem gleichschenkligen Dreieck ist die Mittelsenkrechte der Basis eine Spiegelachse. | ||
| + | Triff dies den Kern des Basiswinkelsatzes? --[[Benutzer:Koooky|Koooky]] 15:45, 6. Jul. 2011 (CEST) | ||
Version vom 6. Juli 2011, 14:45 Uhr
Formulieren Sie den Basiswinkelsatz (Satz VII.5) auf zwei weitere Arten und Weisen.
Ich hoffe ich habe die Aufgabe richtig verstande.
Basiswinkelsatz V1:
Sei  ein gleichschenkliges Dreieck
ein gleichschenkliges Dreieck die Basiswinkel sind kongruent.
die Basiswinkel sind kongruent.
Basiswinkelsatz V2:
Sei  ein Dreieck, wenn
ein Dreieck, wenn 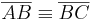 dann gilt
dann gilt 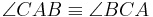 .
.
--Peterpummel 21:01, 2. Jul. 2011 (CEST)
In jedem gleichschenkligen Dreieck ist die Mittelsenkrechte der Basis eine Spiegelachse. Triff dies den Kern des Basiswinkelsatzes? --Koooky 15:45, 6. Jul. 2011 (CEST)

