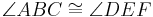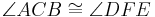Dreieckskongruenz (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Der Kongruenzsatz SSS)
(→‎Der Kongruenzsatz SSS)
Zeile 147: Zeile 147:
  
  
−
Ich komme mit der Schreibweise hier nicht zurecht hoffe man erkennt was ich gemeint hab.<br />
+
Ich komme mit der Schreibweise hier nicht zurecht hoffe man erkennt was ich gemeint hab.<br /><br /><br />
 
Die Schlussfolgerungen in den Schritten 5 und 6 ergeben für mich keinen Sinn, da du ja schon in Schritt 1 <math>\overline{EF*}</math> so konstruierst, dass <math>\overline{BC} \cong \overline{EF*}</math> ist!?--[[Benutzer:Matthias|Matthias]] 13:05, 16. Jul. 2011 (CEST)
 
Die Schlussfolgerungen in den Schritten 5 und 6 ergeben für mich keinen Sinn, da du ja schon in Schritt 1 <math>\overline{EF*}</math> so konstruierst, dass <math>\overline{BC} \cong \overline{EF*}</math> ist!?--[[Benutzer:Matthias|Matthias]] 13:05, 16. Jul. 2011 (CEST)

Version vom 16. Juli 2011, 12:05 Uhr

Inhaltsverzeichnis

Die beiden grundlegenden Ideen der Kongruenz

Bewegungsgeometrie

naive Deckungsgleichheit

Bewegungen: abstandserhaltende Abbildungen der Ebene auf sich

Euklid lässt grüßen: Dreieckskongruenz

Videos zur Idee der Kongruenz

Streckenkongruenz

Wir erinnern uns an die Diskussion zu Anfang des Semesters.

1. Wie sagt man es richtig?

Die Strecken \overline{AB} und \overline{CD} sind kongruent zueinander.
Der Punkt \ A hat zum Punkt \ B denselben Abstand wie der Punkt \ C zum Punkt \ D
Die Strecken \overline{AB} und \overline{CD} haben dieselbe Länge.

Punkte: 0 / 0


Die Auswertung des Quiz zeigt: Alle drei Aussagen sind synonym.

Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz.

Definition VII.1: (Streckenkongruenz)
Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
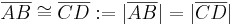
In Zeichen \overline{AB} \cong \overline{CD} := |\overline{AB}| = |\overline{CD}|
Satz VII.1:
Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.

Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.

Winkelkongruenz

Analog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben.

Definition VII.2 : (Winkelkongruenz)
Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
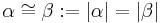
In Zeichen: \alpha \cong \beta := | \alpha | = | \beta |
Satz VII.2:
Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.

Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.

Dreieckskongruenz

In der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen.

Definition VII.3: (Dreieckskongruenz)
Wenn für zwei Dreiecke \overline{ABC} und \overline{DEF} die folgenden 6 Kongruenzen
  1. \overline{AB} \cong \overline{DE}
  2. \overline{BC} \cong \overline{EF}
  3. \overline{AC} \cong \overline{DF}
  4. \angle CAB \cong \angle FDE
  5. \angle ABC \cong \angle DEF
  6. \angle ACB \cong \angle DFE
gelten,
dann sind die beiden Dreiecke \overline{ABC} und \overline{DEF} kongruent zueinander.
Satz VII.3:
Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.

Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.


Überprüfen Sie Ihr Verständnis:

In den Schullehrbüchern findet man häufig Konstruktionsaufgaben wie:
konstruiere das Dreieck mit den Seitenlängen 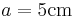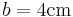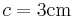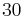\ a = 5\operatorname{cm}, \ b = 4\operatorname{cm}, \ c = 3\operatorname{cm}. \ 30 Schüler konstruieren aufgrund dieser Aufgabenstellung 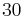\ 30 Dreiecke. Kommentieren Sie den bestimmten Artikel in der Aufgabenstellung. Was hat das alles mit der Idee der Repräsentantenunabhängigkeit zu tun?

Das Kongruenzaxiom SWS

Axiom V: (Kongruenzaxiom SWS)
Wenn für zwei Dreiecke \overline{ABC} und \overline{DEF} die folgenden 3 Kongruenzen
  1. \overline{AB} \cong \overline{DE}
  2. \overline{AC} \cong \overline{DF}
  3. \angle CAB \cong \angle FDE
gelten,
dann sind die beiden Dreiecke \overline{ABC} und \overline{DEF} kongruent zueinander.

Der Kongruenzsatz WSW

Satz VII.4: (Kongruenzsatz WSW)
Wenn für zwei Dreiecke \overline{ABC} und \overline{DEF} die folgenden 3 Kongruenzen
  1. \overline{AB} \cong \overline{DE}
  2. \angle CAB \cong \angle FDE
  3. \angle ABC \cong \angle DEF
gelten,
dann sind die beiden Dreiecke \overline{ABC} und \overline{DEF} kongruent zueinander.
Beweis von Satz VII.4
Als Folge von Tafeln

Der fotografierte Beweis

Video
Die Beweisidee

Testen Sie Ihr Verständnis: Beschreiben Sie hier mit drei ganz einfachen Sätzen, auf welcher Idee der Beweis beruht.


Der Kongruenzsatz SSS

Hier dürfen und sollen Sie sich austoben. Für den Beweis des Kongruenzsatzes SSS werden Sie sinnvollerweise den Basiswinkelsatz benötigen. Weil dieser jedoch von so zentraler Bedeutung ist, haben wir ihm einen eigenen Unterpunkt auf der Hauptseite spendiert. Sie dürfen ihn also hier vorab als wahr voraussetzen.



Zwei Dreiecke ABC und DEF sind zueinander kongruent, wenn sie in allen drei Seiten übereinstimmen.

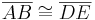
\overline{AB} \cong \overline{DE}
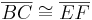
\overline{BC} \cong \overline{EF}
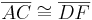
\overline{AC} \cong \overline{DF}

--Teufelchen 13:59, 12. Jul. 2011 (CEST)


Beweisversuch (aber ohne Basiswinkelsatz: geht das so auch?):

Vor. Zwei Dreiecke 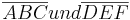\overline{ABC} und \overline {DEF}

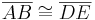
(1) \overline{AB} \cong \overline{DE}
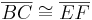
(2) \overline{BC} \cong \overline{EF}
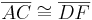
(3) \overline{AC} \cong \overline{DF}


Beh: 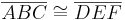\overline{ABC} \cong \overline {DEF}

Es genügt zu zeigen: 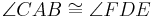\angle CAB \cong \angle FDE weil SWS bereits als Axiom festgelegt

Annahme: oBdA 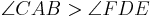\angle CAB > \angle FDE

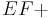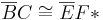
1) Auf EF+ gibt es einen Punkt F* | Ax. v. Lineal \overline BC \cong \overline EF*

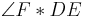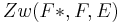
2) F ist Element des Inneren von \angle F*DE und Zw(F*,F,E)

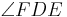3) \angle FDE ist nicht kongruent zu 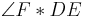\angle F*DE | 2) und Folgerung aus dem Winkeladd.ax.

4) 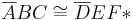\overline ABC \cong \overline DEF* | SWS, Vor (1), Vor.

5) 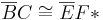\overline BC \cong \overline EF* | 4)

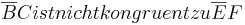6) \overline BC ist nicht kongruent zu \overline EF | 5),3)

das ist ein Widerspruch zur Vor.(2) also müssen die beiden Dreiecke kongruent zueinander sein.


Ich komme mit der Schreibweise hier nicht zurecht hoffe man erkennt was ich gemeint hab.


Die Schlussfolgerungen in den Schritten 5 und 6 ergeben für mich keinen Sinn, da du ja schon in Schritt 1 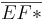\overline{EF*} so konstruierst, dass 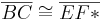\overline{BC} \cong \overline{EF*} ist!?--Matthias 13:05, 16. Jul. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Dreieckskongruenz_(SoSe_11)&oldid=8251“