Lösung von Aufg. 13.4 (SoSe 11): Unterschied zwischen den Versionen
(→Beweisdarstellung 1) |
|||
| Zeile 21: | Zeile 21: | ||
<math>\ oBdA: \ | \overline{AC} \ | \ < \ | \overline{BC} </math><br><br> | <math>\ oBdA: \ | \overline{AC} \ | \ < \ | \overline{BC} </math><br><br> | ||
<math>\ 1) \ | \beta \ | \ < \ | \alpha \ |</math> Annahme, Satz größere Seite liegt dem größeren Winkel gegenüber <br> | <math>\ 1) \ | \beta \ | \ < \ | \alpha \ |</math> Annahme, Satz größere Seite liegt dem größeren Winkel gegenüber <br> | ||
| − | Widerspruch zur Vor. Die Annahme ist zu verwerfen. --[[Benutzer:Phil86|-phil-]] 23:07, 17. Jul. 2011 (CEST) | + | Widerspruch zur Vor. Die Annahme ist zu verwerfen. --[[Benutzer:Phil86|-phil-]] 23:07, 17. Jul. 2011 (CEST)<br /> |
| + | Das geht auch so, sofern der Satz über die gegenüberliegenden Seiten ohne die Verwendung der Umkehrung des Basiswinkelsatzes bewiesen wurde. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:42, 18. Jul. 2011 (CEST) | ||
Aktuelle Version vom 18. Juli 2011, 18:42 Uhr
Beweisen Sie die Gültigkeit der Umkehrung des Basiswinkelsatzes
Hallo - kann jemand eine gültige Lösung einstellen, da wir uns in unserer Übung nicht ganz einig über
die Beweisidee waren.--mm_l 11:26, 14. Jul. 2011 (CEST)
Beweisdarstellung 1
Die Idee des Beweises ist korrekt: Es wird versucht, über die Mittelsenkrechte der Seite 
den Beweis zu führen. Die Darstellung des Beweises ist in einigen Punkten suboptimal.--*m.g.* 18:51, 17. Jul. 2011 (CEST)
meiner ist auch schön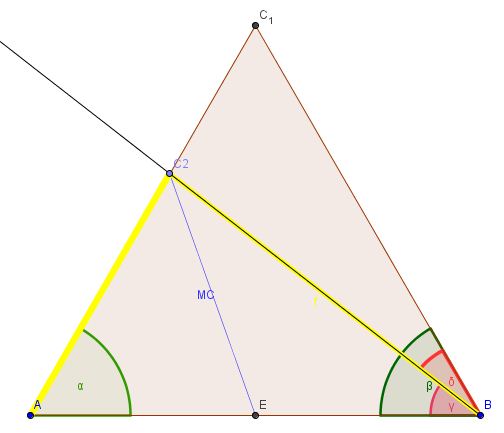
--
Eng.MODs 23:20, 17. Jul. 2011 (CEST)
Gehts auch so? Nur so ne Idee:
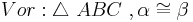
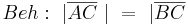
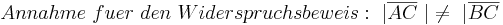
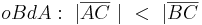
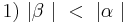Annahme, Satz größere Seite liegt dem größeren Winkel gegenüber
Widerspruch zur Vor. Die Annahme ist zu verwerfen. ---phil- 23:07, 17. Jul. 2011 (CEST)
Das geht auch so, sofern der Satz über die gegenüberliegenden Seiten ohne die Verwendung der Umkehrung des Basiswinkelsatzes bewiesen wurde. --Tutorin Anne 19:42, 18. Jul. 2011 (CEST)
