Diskussion:Streckenantragen oder das Axiom vom Lineal (SoSe 11): Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Wird eigentlich durch das Axiom vom Lineal unsere Axiome I/1 und I/2 "wertlos"? Mir ist zwar klar, dass es was anderes ist, wenn ich eine Gerade habe, dass diese …“) |
Haegar (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
|} | |} | ||
| − | Das müsste es gewesen sein :-) --[[Benutzer:HecklF|Flo60]] 09:47, 5. Jun. 2011 (CEST) | + | Das müsste es gewesen sein :-) --[[Benutzer:HecklF|Flo60]] 09:47, 5. Jun. 2011 (CEST)<br /><br /><br /><br /><br /> |
| + | Wäre es auch Korrekt den Beweis zur Eindeutigkeit eines Mittelpunkts M auf einer Strecke AB folgendermaßen zu führen?:<br /> | ||
| + | |||
| + | Sei M ein Punkt auf der Strecke AB, genauer: Zw(A,M,B). Siehe Definition Zwischenrelation.<br /> | ||
| + | Nach Axiom II/1 gibt es für M eine Zahl d; Der Abstand zu A und eine Zahl d'; der Abstand zu B.<br /> | ||
| + | Ich wähle M so, dass d kongruent zu d' und mit Axiom II/1 und vor allem III/1 ist die Eindeutigkeit dieses Punktes Bewiesen. | ||
| + | |||
| + | Danke schonmal --[[Benutzer:Haegar|Haegar]] 19:10, 22. Jul. 2011 (CEST) | ||
Aktuelle Version vom 22. Juli 2011, 18:10 Uhr
Wird eigentlich durch das Axiom vom Lineal unsere Axiome I/1 und I/2 "wertlos"? Mir ist zwar klar, dass es was anderes ist, wenn ich eine Gerade habe, dass diese min. zwei Punkte enthält. Ich brauche sie lediglich noch 1 mal soweit ich mir vorstellen kann und zwar genau für diesen Satz (den ich mir grad selbst überlegt habe - darauf will ich hier eigentlich hinaus):
Für jeden Punkt P existiert wenigstens eine Gerade, die diesen Punkt enthält.
Voraussetzung: Punkt P
Behauptung: Es existiert wenigstens eine Gerade g mit 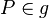
Beweis:
| 1 | 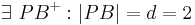 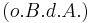 |
Axiom vom Lineal, Voraussetzung |
| 2 | 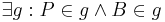 |
(1), Axiom I.1 (so und das wars dann wohl mit Axiom I.1 - jetzt reicht schon ein Punkt und einen zweiten, den ich mir selbst generieren kann um eine Gerade zu erstellen) |
Das müsste es gewesen sein :-) --Flo60 09:47, 5. Jun. 2011 (CEST)
Wäre es auch Korrekt den Beweis zur Eindeutigkeit eines Mittelpunkts M auf einer Strecke AB folgendermaßen zu führen?:
Sei M ein Punkt auf der Strecke AB, genauer: Zw(A,M,B). Siehe Definition Zwischenrelation.
Nach Axiom II/1 gibt es für M eine Zahl d; Der Abstand zu A und eine Zahl d'; der Abstand zu B.
Ich wähle M so, dass d kongruent zu d' und mit Axiom II/1 und vor allem III/1 ist die Eindeutigkeit dieses Punktes Bewiesen.
Danke schonmal --Haegar 19:10, 22. Jul. 2011 (CEST)

