Lösung von Aufg. 14.5 (SoSe 11): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | |||
Beweisen Sie den starken Außenwinkelsatz.<br /><br /> | Beweisen Sie den starken Außenwinkelsatz.<br /><br /> | ||
| Zeile 11: | Zeile 12: | ||
Das könnte man jetzt noch an den anderen beiden Ecken durchexerzieren, aber dafür sollte o.B.d.A. reichen, weil ich ja eigentlich die Ecken benennen kann wie ich möchte und in meinem Beweis nie Bezug auf "längere Seite" o.ä. genommen haben. Richtig? Zu knapp? --[[Benutzer:WikiNutzer|WikiNutzer]] 22:29, 25. Jul. 2011 (CEST)<br /><br /> | Das könnte man jetzt noch an den anderen beiden Ecken durchexerzieren, aber dafür sollte o.B.d.A. reichen, weil ich ja eigentlich die Ecken benennen kann wie ich möchte und in meinem Beweis nie Bezug auf "längere Seite" o.ä. genommen haben. Richtig? Zu knapp? --[[Benutzer:WikiNutzer|WikiNutzer]] 22:29, 25. Jul. 2011 (CEST)<br /><br /> | ||
| + | Bei 1. könnte man vielleicht von Außenwinkel sprechen, wir wollen ja den Außenwinkelsatz beweisen...und dann würd ich als Begründung Definition Außenwinkel schreiben?!--[[Benutzer:Verteidigungswolf|Verteidigungswolf]] 08:25, 26. Jul. 2011 (CEST) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 26. Juli 2011, 07:25 Uhr
Beweisen Sie den starken Außenwinkelsatz.
Innenwinkelsatz für Dreiecke ist bewiesen (und Betragsstriche bei Winkelgrößen etc. sind nicht so wichtig).
Voraussetzung: Dreieck mit den schulüblichen Bezeichnungen
Behauptung: Jeder Außenwinkel ist so groß wie die Summe der nichtanliegenden Innenwinkel.
Beweis:
1. Hilfskonstruktion: Nebenwinkel eines Innenwinkels (nennen wir ihn 
), o.B.d.A. sei es der Nebenwinkel von 
. Begründung: Dreieck hat automatisch Nebenwinkel (brauche ich diese Begründung?)
2. Es gilt: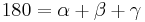 
. Begründung: Innenwinkelsatz für Dreiecke.
3. Es gilt außerdem: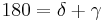 
. Begründung: ist Nebenwinkel von und Nebenwinkel sind nach dem Supplementaxiom supplementär, was heißt: ihre Summe beträgt 180.
4. Damit muss genauso groß sein wie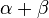 
. Begründung: Rechnen in 
.
Das könnte man jetzt noch an den anderen beiden Ecken durchexerzieren, aber dafür sollte o.B.d.A. reichen, weil ich ja eigentlich die Ecken benennen kann wie ich möchte und in meinem Beweis nie Bezug auf "längere Seite" o.ä. genommen haben. Richtig? Zu knapp? --WikiNutzer 22:29, 25. Jul. 2011 (CEST)
Bei 1. könnte man vielleicht von Außenwinkel sprechen, wir wollen ja den Außenwinkelsatz beweisen...und dann würd ich als Begründung Definition Außenwinkel schreiben?!--Verteidigungswolf 08:25, 26. Jul. 2011 (CEST)
