Lösung von Aufgabe 1.1 (WS 11 12): Unterschied zwischen den Versionen

Version vom 18. Oktober 2011, 14:36 Uhr

In welchen Fällen handelt es sich um Definitionen? Begründen Sie!

1. Jedes n-Eck mit n=4 heißt Viereck.
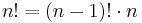2. , falls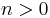
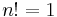   , falls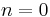
   
3. Stufenwinkel an geschnittenen Parallelen sind kongruent.
4. Jedes Dreieck mit einem Umkreis heißt Sehnendreieck.
5. Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
6. Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
7. Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
8. Jedes Viereck mit einem Umkreis heißt Sehnenviereck.
9. Es gibt Sehnenvierecke.
10. Punkt vor Strich.
11. Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
12. Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
13. Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
14. Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
15. Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
16. Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
17. Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
18. Ein Rechteck hat vier rechte Innenwinkel.
19. Ein Quadrat ist ein Rechteck.
20. Jedes Quadrat ist ein Rechteck.
21. Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.

Ideen und Anregungen

• Wir (die Dienstagsübung) haben ein Problem mit 10. ("Punkt vor Strich.") Das ist ja eine Regel. Können/müssen Regeln definiert werden? --Spannagel 15:36, 18. Okt. 2011 (CEST)
  • Ich habe auch keine Ahnung. --Spannagel 15:36, 18. Okt. 2011 (CEST)