Serie 03: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.3) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.3) |
||
| Zeile 5: | Zeile 5: | ||
Es sei <math>X=\left\{ (x,0)|x\in \mathbb{R} \right\}</math>. Wir definieren auf <math>X</math> die folgende Abbildung <math>\varphi</math>: <math>\forall (x,0) \in X: \varphi((x,0))=(x, \sin^2x)</math>. Jedes Element des <math>\mathbb{R}^2</math> fassen wir als Punkt auf. Hat <math>\varphi</math> Fixpunkte? Wenn ja welche? (Geogebra hilft) | Es sei <math>X=\left\{ (x,0)|x\in \mathbb{R} \right\}</math>. Wir definieren auf <math>X</math> die folgende Abbildung <math>\varphi</math>: <math>\forall (x,0) \in X: \varphi((x,0))=(x, \sin^2x)</math>. Jedes Element des <math>\mathbb{R}^2</math> fassen wir als Punkt auf. Hat <math>\varphi</math> Fixpunkte? Wenn ja welche? (Geogebra hilft) | ||
==Aufgabe 3.3== | ==Aufgabe 3.3== | ||
| − | Unter der Menge aller Punkte wollen wir die Menge aller Pixel eines LCD-Bildschirms <math>B</math> mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel <math>P </math>hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten <math>\left(x_p, y_p\right)</math>. Wir definieren auf den Pixeln unseres Bildschirms <math>B</math> die folgende Abbildung <math>\varphi</math>: <math>\forall P \in B: \varphi(P)=\left(\operatorname zufallsbereich(0;1920),\operatorname zufallsbereich(0;1080)\right)</math> | + | Unter der Menge aller Punkte wollen wir die Menge aller Pixel eines LCD-Bildschirms <math>B</math> mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel <math>P </math>hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten <math>\left(x_p, y_p\right)</math>. Wir definieren auf den Pixeln unseres Bildschirms <math>B</math> die folgende Abbildung <math>\varphi</math>: <math>\forall P \in B: \varphi(P)=\left(\operatorname zufallsbereich(0;1920),\operatorname zufallsbereich(0;1080)\right)</math>. Wie groß ist die Wahrscheinlichkeit, dass <math>\varphi</math> einen Fixpunkt hat? |
==Aufgabe 3.1== | ==Aufgabe 3.1== | ||
Version vom 8. November 2011, 13:16 Uhr
Inhaltsverzeichnis |
Aufgabe 3.1
(alles in ein und derselben Ebene)
Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  und dem Radius
und dem Radius  . Ferner sei
. Ferner sei  eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei
eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei  der gemeinsame Schnittpunkt der Senkrechten in
der gemeinsame Schnittpunkt der Senkrechten in  auf
auf  mit
mit  . Wir definieren eine Abbildung
. Wir definieren eine Abbildung  von
von 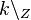 auf
auf  :
: 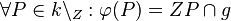 . Ist
. Ist  fixpunktfrei?
fixpunktfrei?
Aufgabe 3.2
Es sei 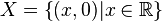 . Wir definieren auf
. Wir definieren auf 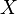 die folgende Abbildung
die folgende Abbildung  :
: 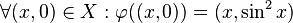 . Jedes Element des
. Jedes Element des 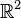 fassen wir als Punkt auf. Hat
fassen wir als Punkt auf. Hat  Fixpunkte? Wenn ja welche? (Geogebra hilft)
Fixpunkte? Wenn ja welche? (Geogebra hilft)
Aufgabe 3.3
Unter der Menge aller Punkte wollen wir die Menge aller Pixel eines LCD-Bildschirms  mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel
mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel  hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten
hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten 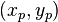 . Wir definieren auf den Pixeln unseres Bildschirms
. Wir definieren auf den Pixeln unseres Bildschirms  die folgende Abbildung
die folgende Abbildung  :
: 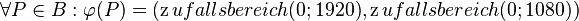 . Wie groß ist die Wahrscheinlichkeit, dass
. Wie groß ist die Wahrscheinlichkeit, dass  einen Fixpunkt hat?
einen Fixpunkt hat?
Aufgabe 3.1
Beweisen Sie: wenn eine Bewegung  zwei verschiedene Fixpunkte
zwei verschiedene Fixpunkte  und
und  hat, dann hat ist die Gerade
hat, dann hat ist die Gerade  eine Fixpunktgerade bezüglich
eine Fixpunktgerade bezüglich  .
.
Aufgabe 3.2
Beweisen Sie: Wenn drei nicht kollineare Punkte  Fixpunkte der Bewegung
Fixpunkte der Bewegung  sind, so ist
sind, so ist  die identische Abbildung.
==
die identische Abbildung.
==

