Lösung von Aufg. 6.6 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „<u>'''Satz:'''</u> :Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear. # Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen…“)
 
Zeile 13: Zeile 13:
  
  
 +
<br /><br />
 +
zu 1. Wenn vier Punkte nicht in einer Ebene liegen, dann liegen je drei von ihnen nicht auf einer Geraden.<br />
 +
zu 2. Liegen vier Punkte nicht in einer Ebene gilt für drei davon, dass sie nicht auf einer Geraden liegen. <br />
 +
zu 3.
 +
<u>'''Beweis'''</u>
 +
Voraussetzung::Es seien <math>\ A, B, C</math> und <math>\ D</math> vier Punkte, die nicht komplanar sind.
 +
<u>'''zu zeigen'''</u>
 +
:: o.B.d.A. : A, B, C nicht kollinear
 +
<u>'''Annahme:'''</u>
 +
::Es gibt drei Punkte von den vier Punkten <math>\ A, B, C, D</math>, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte A,B,C sein.
 +
 +
 +
{| class="wikitable"
 +
|-
 +
| Beweisschritt || Begründung
 +
|-
 +
| (1)koll(A,B,C)  || Annahme
 +
|-
 +
| (2)Es existiert eine Gerdade g mit A,B,C Element g || (1) Defninition koll
 +
|-
 +
| (3) Zwei Punkte der Geraden und der Punkt D liegen in einer Ebene || Axiom I/4
 +
|-
 +
| (4) Die drei Punkte der Geraden gehören ebenfalls zu dieser Ebene || Axiom I/5
 +
|-
 +
| (5) komp(A,B,C,D) || (2)(3)(4)
 +
|-
 +
| Wiederspruch zur Voraussetzung, die Annahme ist zu verwerfen.
 +
|}
 +
--[[Benutzer:LGDo12|LGDo12]] 13:35, 17. Nov. 2011 (CET)
  
  
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 17. November 2011, 13:35 Uhr

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
  1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
  2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
  3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

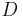Es seien \ A, B, C und \ D vier Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei Punkte von den vier Punkten \ A, B, C, D, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...




zu 1. Wenn vier Punkte nicht in einer Ebene liegen, dann liegen je drei von ihnen nicht auf einer Geraden.
zu 2. Liegen vier Punkte nicht in einer Ebene gilt für drei davon, dass sie nicht auf einer Geraden liegen.
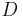zu 3. Beweis Voraussetzung::Es seien \ A, B, C und \ D vier Punkte, die nicht komplanar sind. zu zeigen

o.B.d.A. : A, B, C nicht kollinear

Annahme:

Es gibt drei Punkte von den vier Punkten \ A, B, C, D, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte A,B,C sein.


Beweisschritt Begründung
(1)koll(A,B,C) Annahme
(2)Es existiert eine Gerdade g mit A,B,C Element g (1) Defninition koll
(3) Zwei Punkte der Geraden und der Punkt D liegen in einer Ebene Axiom I/4
(4) Die drei Punkte der Geraden gehören ebenfalls zu dieser Ebene Axiom I/5
(5) komp(A,B,C,D) (2)(3)(4)
Wiederspruch zur Voraussetzung, die Annahme ist zu verwerfen.

--LGDo12 13:35, 17. Nov. 2011 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._6.6_(WS_11/12)&oldid=9436“