Lösung von Aufg. 8.5 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. Kategorie:Einführung_Geometrie“) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | ||
| + | Eine Punktmenge ist konvex, wenn für alle Punkte A und B der Punktmenge gilt, dass alle Punkte der Strecke AB Element der Punktmenge P sind. | ||
| + | |||
| + | Vor: Es sind X und Y zwei konvexe Punktmengen. | ||
| + | |||
| + | Beh: <math>\ X \cap Y</math> ist Konvex | ||
| + | 1. Es seien A und B zwei Punkte aus der Schnittmenge X,Y ( Vor.) | ||
| + | |||
| + | 2. A, B Element X und A, B Element Y und die Schnittmenge ist nicht leer ( Vor.) | ||
| + | |||
| + | 3. <math>\overline{AB} c X und \overline{AB} c von Y (aus 2, vor., Def. konvexe Punktmengen) | ||
| + | </math> | ||
| + | |||
| + | 4. <math>\overline{AB} c X und Y</math> ( 3, Def. Schnittmenge) | ||
| + | |||
| + | 5. X geschnitten Y = konvex (4, Def. konvexe Menge ) | ||
| + | --[[Benutzer:Costa rica|Costa rica]] 23:46, 5. Dez. 2011 (CET) | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 5. Dezember 2011, 23:46 Uhr
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Eine Punktmenge ist konvex, wenn für alle Punkte A und B der Punktmenge gilt, dass alle Punkte der Strecke AB Element der Punktmenge P sind.
Vor: Es sind X und Y zwei konvexe Punktmengen.
Beh: 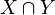 ist Konvex
1. Es seien A und B zwei Punkte aus der Schnittmenge X,Y ( Vor.)
ist Konvex
1. Es seien A und B zwei Punkte aus der Schnittmenge X,Y ( Vor.)
2. A, B Element X und A, B Element Y und die Schnittmenge ist nicht leer ( Vor.)
3. 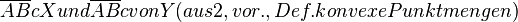
4. 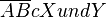 ( 3, Def. Schnittmenge)
( 3, Def. Schnittmenge)
5. X geschnitten Y = konvex (4, Def. konvexe Menge ) --Costa rica 23:46, 5. Dez. 2011 (CET)

