12)

Beweisen Sie: Ein Punkt $\ P$ gehört genau dann zur Winkelhalbierenden des Winkels $\ \alpha$, wenn er zu den Schenkeln von $\ \alpha$ jeweils denselben Abstand hat.

• Dürfen wir SsW benutzen?--Miriam 12:13, 21. Jan. 2012 (CET)
  • Ja, du kannst SsW benutzen. Allerdings musst du dann immer begründen, dass S (lange Seite) wirklich länger als s (kurze Seite) ist. Das ist meist schwer zu zeigen.--Tutorin Anne 13:06, 25. Jan. 2012 (CET)
    
• Wenn man für die Rückrichtung "<-" gezeigt hat, dass 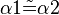$\alpha1 \tilde {=} \alpha2$, also die beiden Winkel, die durch die Winkelhalbierende erzeugt wurden, muss man dann zusätzlich noch zeigen, dass P im Inneren des Winkels liegt? --Todah raba 19:29, 25. Jan. 2012 (CET)
  
  

HILFE!!! Sind wir beim Winkelhalbierendenkriterium in der Euklidischen Geometrie oder in der Absoluten? Dies ist ein echtes Problem, da es für mich eindeutig zur absoluten Geometrie gehört, ich aber die Rückrichtung nicht Ohne Innenwinkelsumme lösen kann.--Adores 00:27, 26. Jan. 2012 (CET)