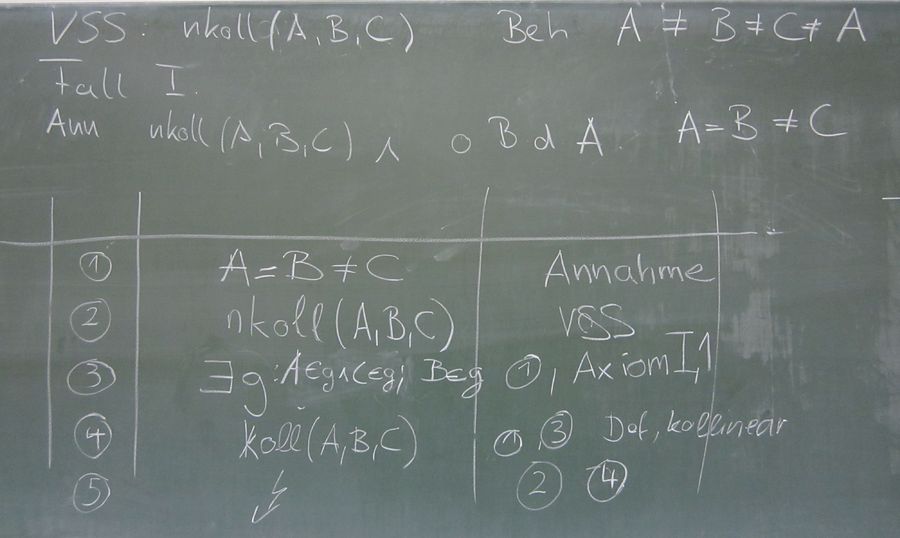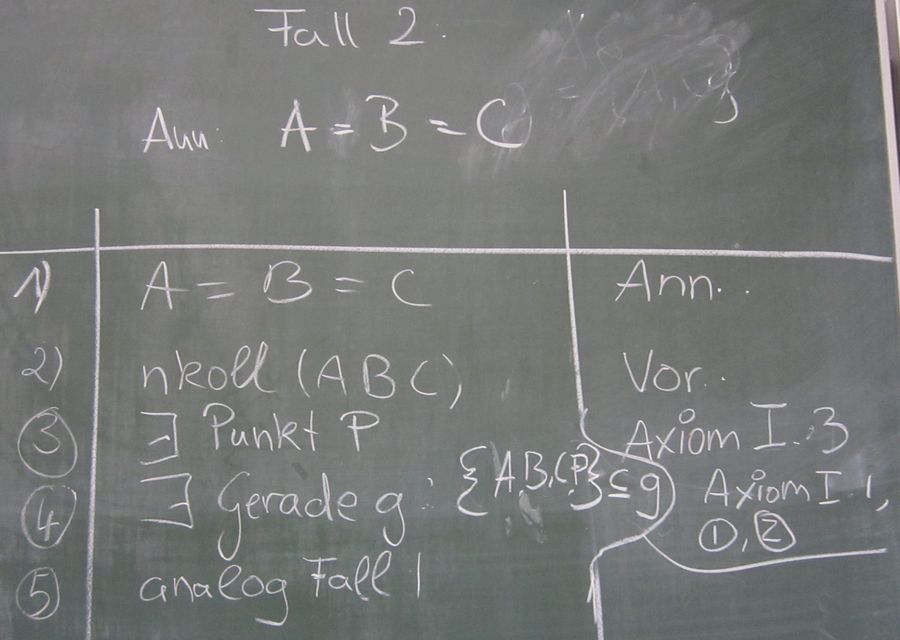Beweisidee Aufgabe 4.3.2 S Übung Heckl (SoSe2012)

Aufgabe 4.3

Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.

1. Wir formulieren Satz I neu und beginnen mit „Es seien $A$, $B$ und $C$ drei Punkte.“ Ergänzen Sie: „Wenn $A$,$B$ und $C$ nicht kollinear sind , dann sind sie paarweise verschieden .“
2. Beweisen Sie Satz I indirekt mit Widerspruch.

Beweis in zwei Fällen (Reihenfolge der Fälle ist irrelevant) durch Widerspruch:

Fall 1: Annahme: Gelte o. B. d. A. A = B $\neq$ C

Fall 2: Annahme: Gelte A = B = C = A

Kommentar zu Fall 2:

Sinnvollerweise schreiben wir zu 3): $\exists P \neq A$, ansonsten könnte es ja sein, dass P = A ist; 

dann kann nämlich Axiom I.1 nicht angewendet werden - diesen Fall schließen wir somit aus und unser Axiom kann angewendet werden,

weil wir zwei verschiedene Punkte haben! --Flo60 20:33, 16. Mai 2012 (CEST)

Zurück zur Übungsseite

Übung Aufgaben 4 S (SoSe 12)