Lösung von Zusatzaufgabe 5.2 P (SoSe 12)
Aus Geometrie-Wiki
Version vom 27. Mai 2012, 16:58 Uhr von Studentin (Diskussion | Beiträge)
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden 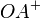 und
und 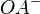 :
:
a)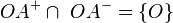 und
und
b)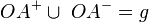
a)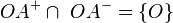
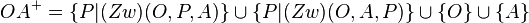
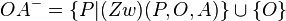
in der schnittmenge gibt es nur ein gemeinsames element: "o"
- es ist noch zu beweisen, dass keine weiteren Punkte außer O in der Schnittmenge liegen. Dies lässt sich am einfachsten indirekt beweisen.--Tutorin Anne 17:13, 27. Mai 2012 (CEST)
muss es noch bewiesen werden? wir wissen doch, dass alle drei zwischenrelationen disjunkt sind...--Studentin 17:58, 27. Mai 2012 (CEST)
b)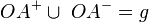
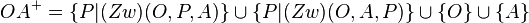
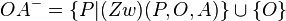
in der vereinigungsmenge ist die gerade g, da in der vereinigungsmenge sowohl die punkte a und o, als auch alle punkte zw (a,o,p), zw (p,o,a), zw (o,p,a) enthalten sind.
--Studentin 16:35, 27. Mai 2012 (CEST)

