Lösung von Aufgabe 9.2P (SoSe 12)
Beweisen Sie die Geradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue der Geradenspiegelung.
ich versteh nicht ganz, was wir beweisen sollen:
wenn wir die halbgeradentreue bewiesen haben, müssen wir die geradentreue doch eigentlich gar nicht mehr beweisen, oder?
eine gerade ab ist doch die vereinigungsmenge der beiden halbgeraden ab+ und ab-
wenn beide halbgeradentreu sind, ist doch die gerade geradentreu...--Studentin 00:47, 25. Jun. 2012 (CEST)
Ja, dann müssen wir evtl einfach noch die Halbgerade AB+ und AB- zusammenfügen und somit zeigen, dass A´B´ existiert. Oder?--PippiLotta 13:57, 25. Jun. 2012 (CEST)
Ja. Die "Geradentreue" müsste dann die Vereinigungsmenge zweier Halbgeraden sein! Aber ich glaube hier müssen wir aufpassen, denn AB+ und AB- sind zwar Halbebenen, aber beide haben den Punkt A. Also müssten wir zwei Halbebenen vereinigen bspw.:  und
und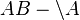 Was sagt ihr dazu? Ist es egal, ob ich AB+ und AB- vereinige, oder muss ich eine Halbgerade ohne {A} haben? --Honeydukes 15:00, 25. Jun. 2012 (CEST)
Was sagt ihr dazu? Ist es egal, ob ich AB+ und AB- vereinige, oder muss ich eine Halbgerade ohne {A} haben? --Honeydukes 15:00, 25. Jun. 2012 (CEST)
ich würde sagen, dass das vollkommen egal ist - denn du hast ja die vereinigungsmenge.--Studentin 16:53, 25. Jun. 2012 (CEST)
Stimmt, danke. --Honeydukes 22:22, 25. Jun. 2012 (CEST)
Sehr gut! So ist es! Und die Begründung von Studentin und PippiLotta sind die Beweisidee für die Gereadentreue - besser ist es noch genau Schritt für Schritt die Aussagen zu führen:--Tutorin Anne 11:58, 26. Jun. 2012 (CEST)
| Voraussetzung | Geradenspiegelung an g 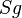 mit mit 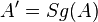 und und 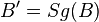 ... ...
|
| Behauptung |
| Beweisschritt | Begründung |
|---|---|
1 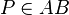 |
(Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |

