Lösung von Aufgabe 9.4P (SoSe 12)

m sei Mittelsenkrechte der Strecke $\overline{AB}$. Beweisen Sie durch Kontraposition und mit Hilfe abbildungsgeometrischer Betrachtungen: $\left| AP \right| =\left| BP \right|\Rightarrow P\in m$


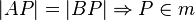
Voraussetzung: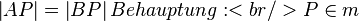
$\left| AP \right| =\left| BP \right| Behauptung:<br /> P\in m$ Kontraposition:
P nicht Element m

Fall 1:

P liegt in der selben HE wie B

1.Strecke BP geschnitten mit m= leere Menge (Def. HE, Ann.)

2. Strecke AP geschnitten mit m= S (1. Def. HE)

3. S ist Element von der Strecke AP (1.2)

4. ZW(A,S,P) (3.)

5. Strecke AS+ Strecke SP= Strecke AP (Def. ZW)

6. Strecke AP ist größer als Strecke BP (Widerspruch zur Vor.)

Fall 2:

P liegt in der selben HE wie A

analog

Hilfreiche Sätze für den Beweis könnten sein: , Dreiecksungleichung
Und eine Skizze hilft auch schon!--Tutorin Anne 15:29, 26. Jun. 2012 (CEST)