Lösung von Aufgabe 6.8

Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.

Nochmal zur Erklärung die Kreisdefinition aus Aufgabe 6.7:
Ein Kreis sei die Menge aller Punkte P_i, die den gleichen Abstand zu Punkt M haben. Diesen Punkt M nennen wir Mittelpunkt des Kreises.
Vorraussetzung: Alle Punkte P_i und der Punkt M liegen in der selben Ebene $\Epsilon$.

Lösung --Schnirch 13:14, 16. Jun. 2010 (UTC)

Eine Strecke $\overline{AB}$ ist dann eine Kreissehne eines Kreises $k$, wenn $A$ und $B$ zu $k$ gehören.

Eine Strecke $\overline{MB}$ ist dann ein Kreisradius eines Kreises $k$, wenn $B$ zu $k$ gehört.

Eine Strecke $\overline{AB}$ ist dann ein Kreisdurchmesser eines Kreises $k$, wenn $A$ und $B$ zu $k$ gehören und $\overline{AB}$ durch den Mittelpunkt $M$ geht.

vorausgegangene Diskussion:

Kreissehnen

Eine Kreissehne ist die Strecke (Verbindung) zwischen zwei Punkten des Kreises: P_j und P_k

Kreisradien

Eine Kreisradius ist die Strecke (Verbindung) zwischen dem Mittelpunkt M des Kreises und einem beliebigen Punkt P_i. (geht mit allen Ps, da Definition Kreis sagt, dass Kreis durch GLEICHEN Abstand definiert ist.

Kreisdurchmesser

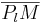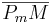Eine Kreisdurchmesser ist die Strecke (Verbindung) zwischen zwei Punkten P_l und P_m, die durch den Mittelpunkt geht. Da es sich also um die addierten Strecken $\overline {P_lM}$ und $\overline {P_mM}$ handelt, ist der Durchmesser immer = doppelter Radius. Echt.

--Heinzvaneugen

zum Kreisdurchmesser:
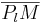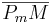muss man nicht noch irgendwie sagen, dass die Strecken $\overline {P_lM}$ und $\overline {P_mM}$ auf ein und derselben Geraden liegen? --Maude001 20:12, 6. Jun. 2010 (UTC)

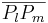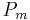@Maude001 Gibt es eine Möglichkeit, eine Strecke $\overline {P_lP_m}$ "ohne Knick" zu zeichnen, die der Definition von Strecke entspricht? Kollinear müssen die Punkte $P_l$ und $P_m$ sein, wenn der Mittelpunkt 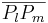$\in$ $\overline {P_lP_m}$ sein soll...
--Heinzvaneugen

@Heinzvaneugen Du hast vollkommen recht, ich habe den Anfang der Definition überlesen!--Maude001 10:42, 8. Jun. 2010 (UTC)