Lösung von Testaufgabe 02
Lösungsversuch Nummero6/Tchu Tcha Tcha:
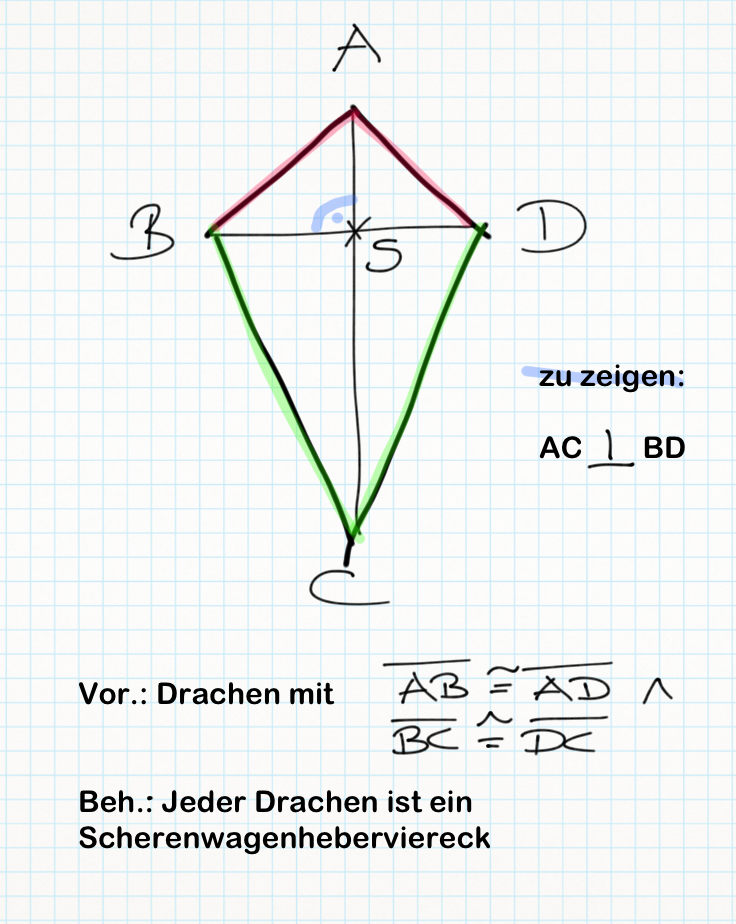
(1) 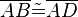 // Vor.
// Vor.
(2) 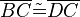 // Vor.
// Vor.
(3) 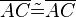 // Vor.
// Vor.
(4) 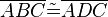 // (1-3), SSS
// (1-3), SSS
(5) 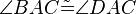 // (4), Dreieckskongruenz
// (4), Dreieckskongruenz
(6) 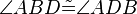 // Vor., Basiswinkelsatz
// Vor., Basiswinkelsatz
(7) 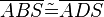 // (5),(1),(6), WSW
// (5),(1),(6), WSW
(8) 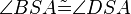 // (7), Dreieckskongruenz
// (7), Dreieckskongruenz
(9) 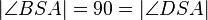 // (8), Def.NW, Def. rechter Winkel
// (8), Def.NW, Def. rechter Winkel
(10) Da 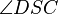 Nebenwinkel von
Nebenwinkel von 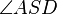 und
und 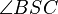 Nebenwinkel von
Nebenwinkel von  ist,
muss nach Def. NW und Def. rechter Winkel gelten:
ist,
muss nach Def. NW und Def. rechter Winkel gelten: 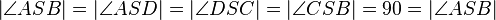
(11) Nach (10) und der Def. senkrecht auf der Menge der Geraden bzw. Strecken wissen wir nun:
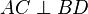
(12) Nach der "Def. Scherenwagenheberviereck" ist auch jeder Drachen wegen (11) ein Scherenwagenheberviereck.
(13) Behauptung stimmt. qed. // (12)
(Hinweis:10 Minuten waren mir mit Zeichnung zu knapp.. eher 15 min :-( )
--Tchu Tcha Tcha 22:02, 8. Jul. 2012 (CEST)
Hier meine Idee:

Bei 4) gehört noch als Begründung "3)" dahinter.
--RitterSport 21:20, 9. Jul. 2012 (CEST)
Das frag' ich mich auch... ;) Def. Raute?!? --Tchu Tcha Tcha 07:58, 10. Jul. 2012 (CEST)
Vielleicht hängt das ja irgendwie mit dem zusammen, dass jede Raute ein spezieller Drache ist und man diesen Beweis
auch hier analog führen könnte...!?!?
Ja genau! Ich habe den Beweis über die Raute geführt. Das ist leichter als über den Drachen zu gehen. Durch die Def. habe ich ja vier kongruente Seiten. Jetzt muss ich nur noch zeigen dass die entstehenden Teildreiecke, bzw ihre Seiten senkrecht aufeinander stehen.
Beweis kommt gleich online.....--Nemo81 17:44, 17. Jul. 2012 (CEST)

